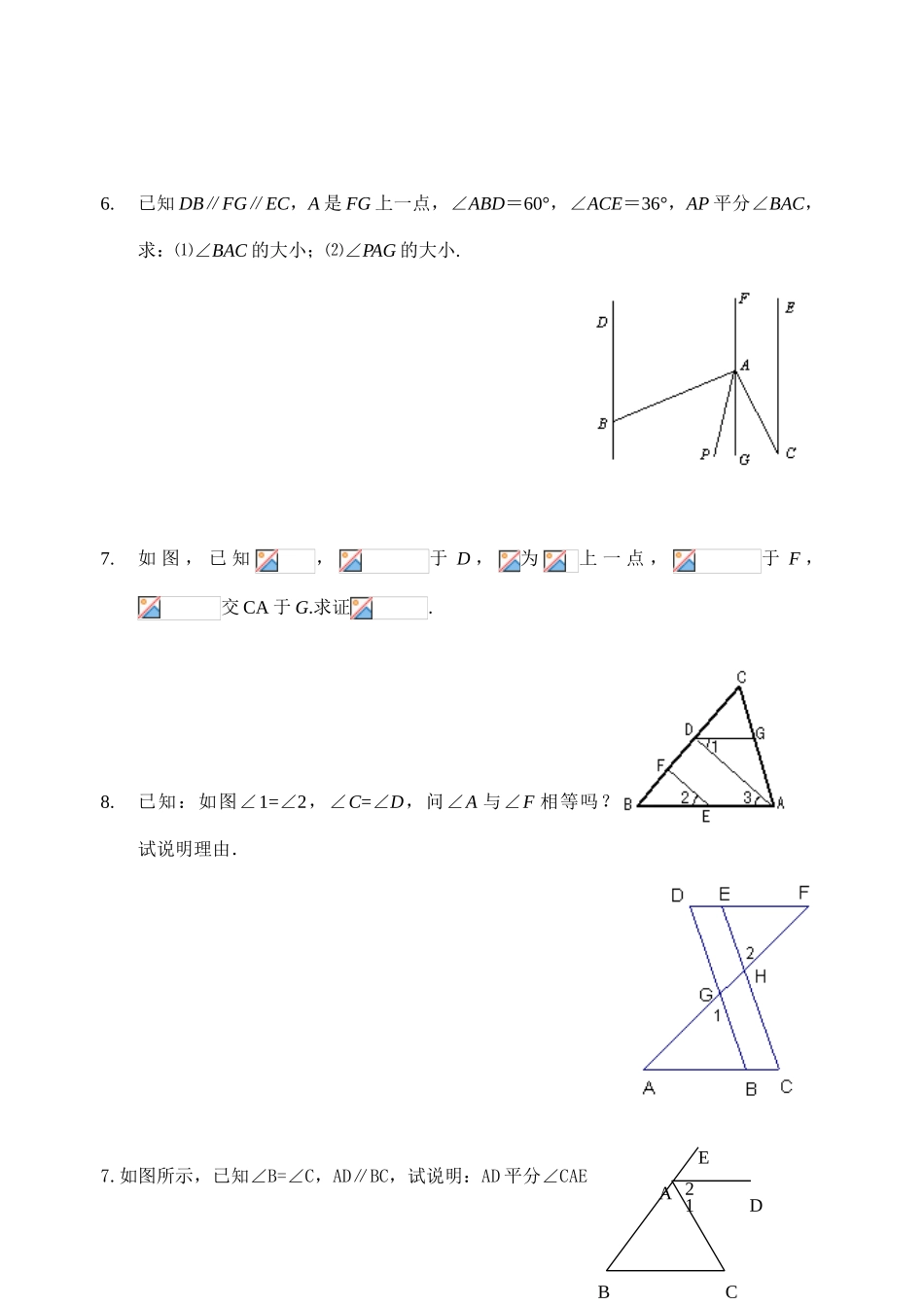
第五章 相交线与平行线 证明题练习熟悉以下各题:1.如 图 ,那 么点A 到 BC 的距离是_____,点 B 到 AC 的距离是_______,点A、B 两点的距离是_____,点 C 到 AB 的距离是________.2.设、b、c 为平面上三条不同直线,a)若,则 a 与 c 的位置关系是_________;b)若,则 a 与 c 的位置关系是_________;c)若,,则 a 与 c 的位置关系是________.3.如图,已知 AB、CD、EF 相交于点 O,AB⊥CD,OG 平分∠AOE,∠FOD=28°,求∠COE、∠AOE、∠AOG 的度数.4.如图,与是邻补角,OD、OE 分别是与的平分线,试推断 OD 与 OE 的位置关系,并说明理由.5.⑴ 如图,已知∠1=∠2 求证:a∥b.⑵直线,求证:.DEABC216.已知 DB∥FG∥EC,A 是 FG 上一点,∠ABD=60°,∠ACE=36°,AP 平分∠BAC,求:⑴∠BAC 的大小;⑵∠PAG 的大小.7.如 图 , 已 知,于 D ,为上 一 点 ,于 F ,交 CA 于 G.求证.8.已知:如图∠1=∠2,∠C=∠D,问∠A 与∠F 相等吗?试说明理由.7.如图所示,已知∠B=∠C,AD∥BC,试说明:AD 平分∠CAEl1lCBDPl2A8、如图所示,已知 AD 是∠EAC 的平分线,AD∥BC,∠B=300求∠DAE,∠DAC,∠C 的度数。(12 分)10.已知:如图 13,AB∥CD,求∠A+∠E+∠C 的度数。2、已知 AD⊥BC,FG⊥BC,垂足分别为 D、G,且∠1=∠2,猜想∠BDE 与∠C 有如何的大小关系?试说明理由.3、 如右图,光线 a 照射到平面镜 CD 上,然后在平面镜 AB 和 CD 之间来回反射,这时间线的入射角等于反射角,即∠1=∠6,∠5=∠3,∠2=∠4。若已知∠1=55°,∠3=75°,求∠2 的度数。4、 如图,已知直线 l1∥l2,直线 l3和直线 l1、l2交于点 CDEABC和 D,在 C、D 之间有一点 P,假如 P 点在 C、D 之间运动时,问∠PAC,∠APB,∠PBD 之间的关系是否发生变化.若点 P 在 C、D 两点的外侧运动时(P 点与点 C、D 不重合),试探究∠PAC,∠APB,∠PBD 之间的关系又是如何? 5、已知 AB∥CD,试再添上一个条件,使∠1=∠2 成立(规定给出两个答案).6、已知:如图,直线 AB∥CD,直线 EF 分别交 AB,CD 于点 E,F,∠BEF 的平分线与∠DFE的平分线相交于点 P.试求∠P 的大小.7、已知 AB//DE,∠ABC=80°,∠CDE=140°,求∠BCD.ABEPFCDEDCBA132AECDBF图 10相交线与平行线证明题1.已知:如图⑿,CE 平分∠ACD,∠1=∠B,求证:AB∥C...