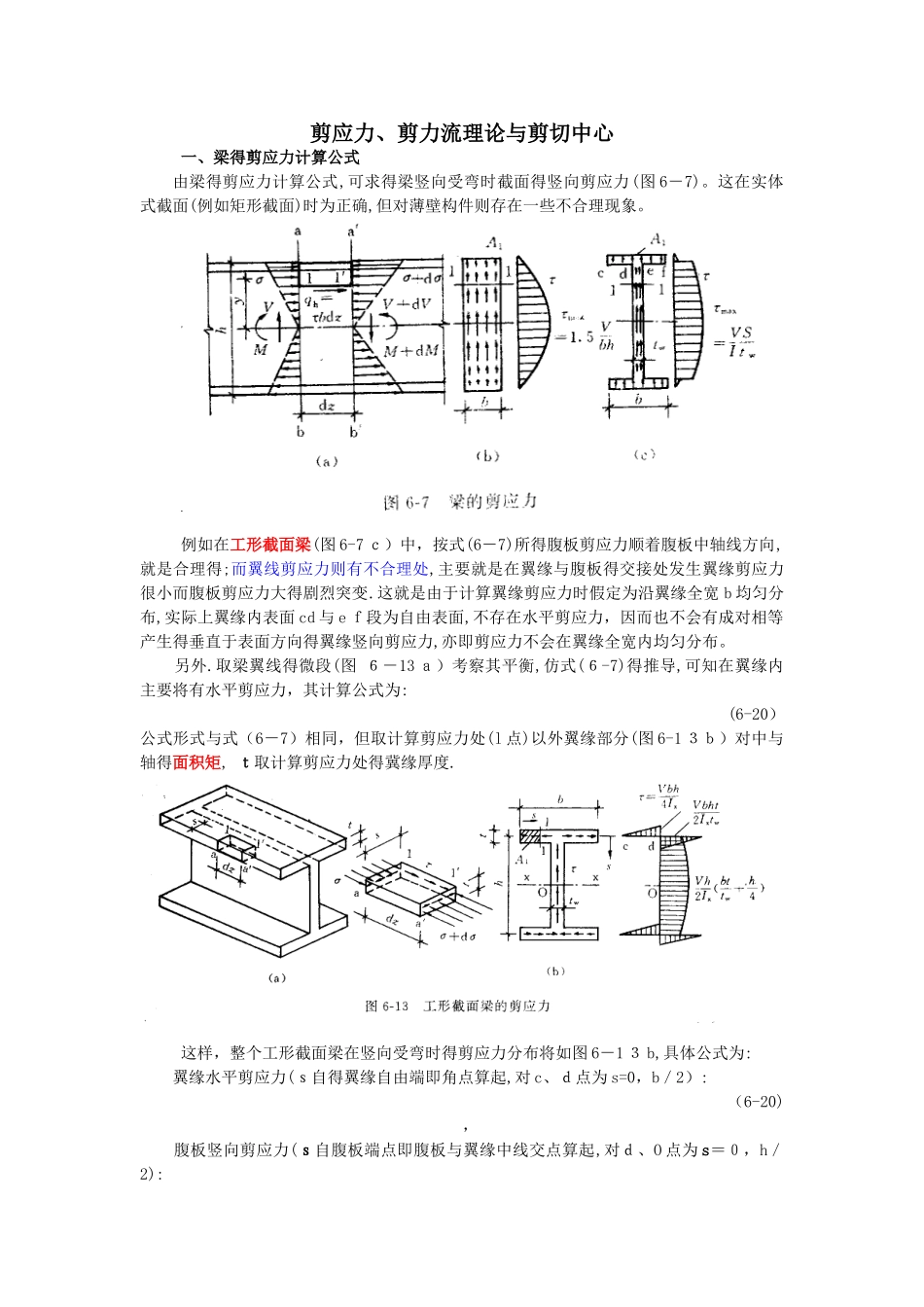
剪应力、剪力流理论与剪切中心 一、梁得剪应力计算公式由梁得剪应力计算公式,可求得梁竖向受弯时截面得竖向剪应力(图 6-7)。这在实体式截面(例如矩形截面)时为正确,但对薄壁构件则存在一些不合理现象。 例如在工形截面梁(图 6-7 c)中,按式(6-7)所得腹板剪应力顺着腹板中轴线方向,就是合理得;而翼线剪应力则有不合理处,主要就是在翼缘与腹板得交接处发生翼缘剪应力很小而腹板剪应力大得剧烈突变.这就是由于计算翼缘剪应力时假定为沿翼缘全宽 b 均匀分布,实际上翼缘内表面 cd 与 e f段为自由表面,不存在水平剪应力,因而也不会有成对相等产生得垂直于表面方向得翼缘竖向剪应力,亦即剪应力不会在翼缘全宽内均匀分布。 另外.取梁翼线得微段(图 6-13 a)考察其平衡,仿式(6-7)得推导,可知在翼缘内主要将有水平剪应力,其计算公式为: (6-20)公式形式与式(6-7)相同,但取计算剪应力处(l 点)以外翼缘部分(图 6-1 3b)对中与轴得面积矩, t取计算剪应力处得冀缘厚度. 这样,整个工形截面梁在竖向受弯时得剪应力分布将如图 6-1 3 b,具体公式为: 翼缘水平剪应力(s自得翼缘自由端即角点算起,对 c、d点为 s=0,b/2): (6-20) , 腹板竖向剪应力(s自腹板端点即腹板与翼缘中线交点算起,对d、O 点为 s=0,h/2): (6-20) , 注意所有剪应力都在顺着薄壁截面得中轴线S方向,并为同一流向(图 6-1 3b)。容易证明:截面全部剪应力得总合力等于竖向剪力V,水平合力则互相抵消平衡。 二、薄壁构件得剪力流理论 根据上面得推论,可得到薄壁构件受弯时得剪应力分布规律:无论就是竖向、水平或双向受弯,截面各点剪应力均为顺着薄壁截面得中轴线 S 方向(图 6-13b、6-14,示竖向弯曲情况),在与之垂直即壁厚方向得剪应力则很小而可忽略不计;且由于壁薄可假定剪应力 τ 沿厚度 t 为均匀分布,其大小为: , (6-2 3)ﻭ上面左式 τ 即式(6-2 0)得剪应力,右式则就是沿薄壁截面s轴单位长度上得剪力(N/m m)。除了需要验算剪应力得情况外,用一般更为方便有用。 竖向弯曲时上式用,水平弯曲时则用。因二者 τ 得方向均为沿 S 铀,故双向弯曲时二者可直接叠加(考虑正负号)。 将按其方向用箭头线画在薄壁截面中轴线S轴上时,将成为自下向上或自上向下得连续射线(图 6-1 3b、6-14);称为薄壁构件竖向(或水平)弯曲产生得剪力流.这种剪力流在任意截面上都就是连续得,在板件交点...