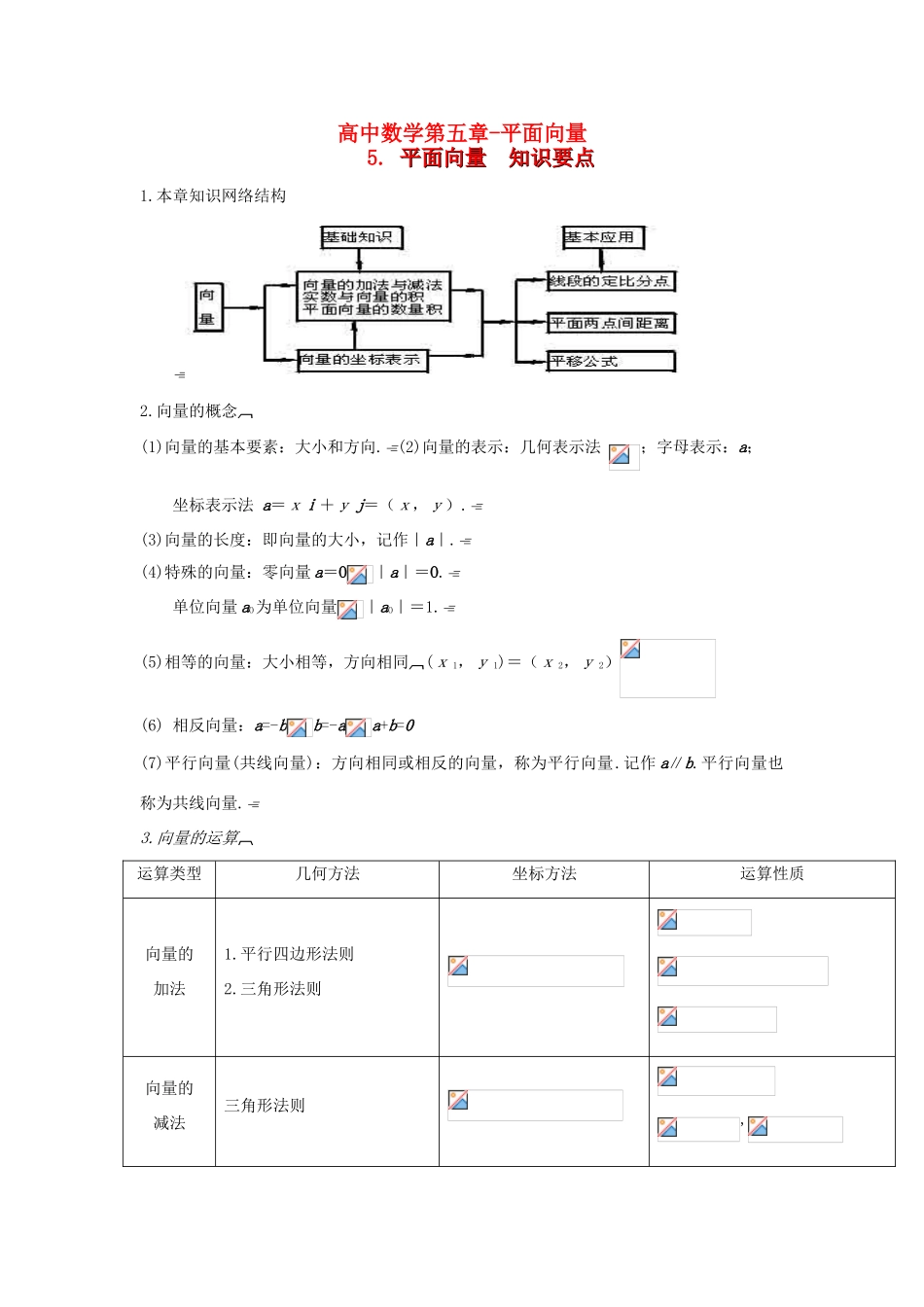
高中数学第五章-平面向量5. 平面向量平面向量 知识要点知识要点1.本章知识网络结构2.向量的概念(1)向量的基本要素:大小和方向.(2)向量的表示:几何表示法 ;字母表示:a;坐标表示法 a=xi+y j=(x,y).(3)向量的长度:即向量的大小,记作|a|.(4)特殊的向量:零向量 a=O|a|=O.单位向量 aO为单位向量|aO|=1.(5)相等的向量:大小相等,方向相同(x 1,y 1)=(x 2,y 2)(6) 相反向量:a=-bb=-aa+b=0(7)平行向量(共线向量):方向相同或相反的向量,称为平行向量.记作 a∥b.平行向量也称为共线向量.3.向量的运算运算类型几何方法坐标方法运算性质向量的加法1.平行四边形法则2.三角形法则向量的减法三角形法则,数乘向量1.是 一 个 向 量 , 满 足 :2.>0 时, 同向;<0 时, 异向;=0 时, .向量的数量积是一个数1.时,.2. 4.重要定理、公式(1)平面向量基本定理e1,e2是同一平面内两个不共线的向量,那么,对于这个平面内任一向量,有且仅有一对实数 λ1,λ2,使 a=λ1e1+λ2e2.(2)两个向量平行的充要条件a∥ba=λb(b≠0)x1y2-x2y1=O.(3)两个向量垂直的充要条件a⊥ba·b=Ox1x2+y1y2=O.(4)线段的定比分点公式设点 P 分有向线段所成的比为 λ,即=λ,则=+ (线段的定比分点的向量公式) (线段定比分点的坐标公式)当 λ=1 时,得中点公式:=(+)或 (5)平移公式设点 P(x,y)按向量 a=(h,k)平移后得到点 P′(x′,y′),则=+a 或曲线 y=f(x)按向量 a=(h,k)平移后所得的曲线的函数解析式为:y-k=f(x-h)(6)正、余弦定理正弦定理:余弦定理:a2=b2+c2-2bccosA,b2=c2+a2-2cacosB,c2=a2+b2-2abcosC.(7)三角形面积计算公式:设△ABC 的三边为 a,b,c,其高分别为 ha,hb,hc,半周长为 P,外接圆、内切圆的半径为 R,r.①S△=1/2aha=1/2bhb=1/2chc ②S△=Pr ③S△=abc/4R④S△=1/2sinC·ab=1/2ac·sinB=1/2cb·sinA ⑤S△= [海伦公式] ⑥S△=1/2(b+c-a)ra[如下图]=1/2(b+a-c)rc=1/2(a+c-b)rb[注]:到三角形三边的距离相等的点有 4 个,一个是内心,其余 3 个是旁心.如图: 图 1 中的 I 为 S△ABC的内心, S△=Pr 图 2 中的 I 为 S△ABC的一个旁心,S△=1/2(b+c-a)ra 附:三角形的五个“心”;重心:三角形三条中线交点.外心:三角形三边垂直平分线相交...