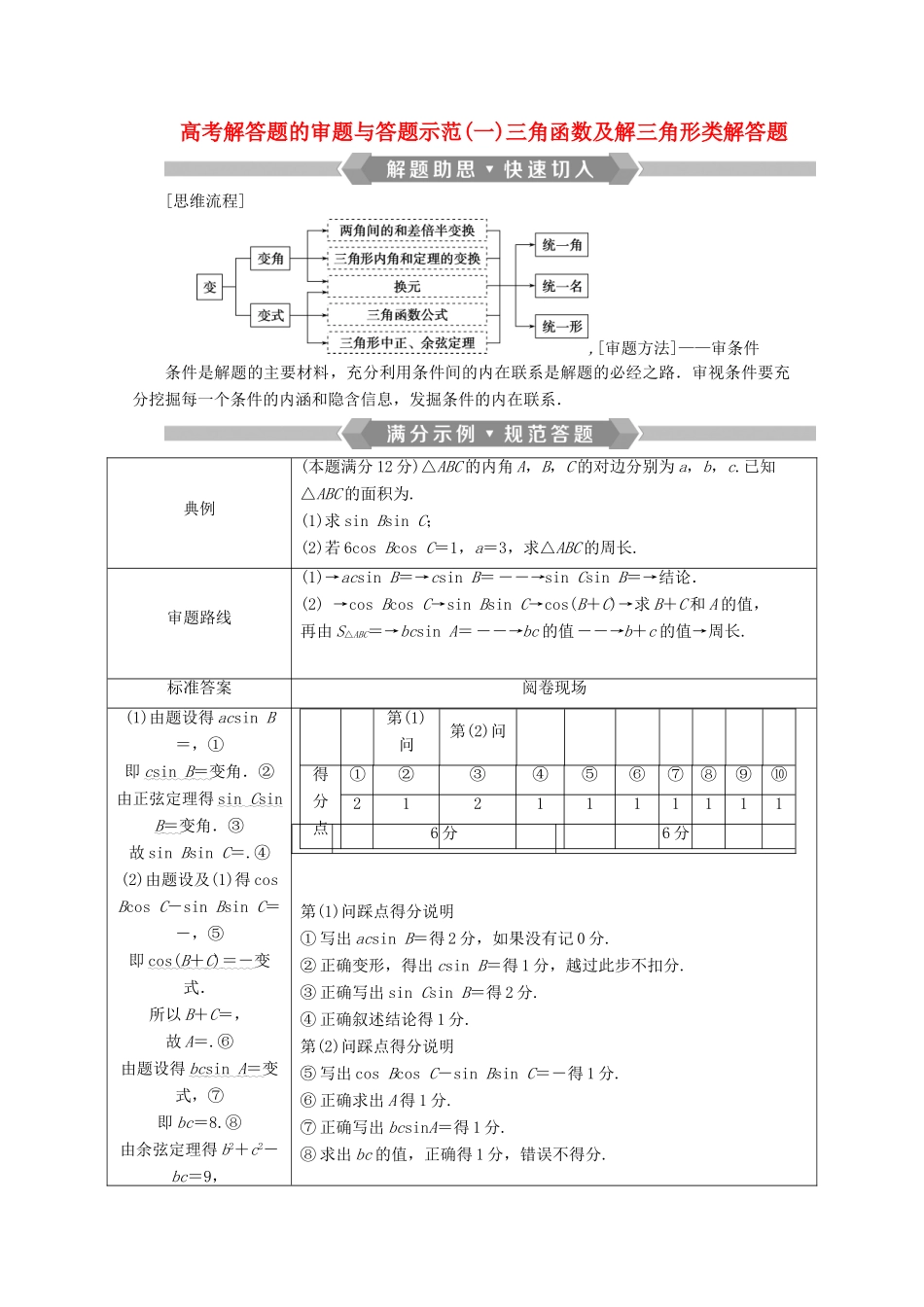
高考解答题的审题与答题示范(一)三角函数及解三角形类解答题[思维流程],[审题方法]——审条件条件是解题的主要材料,充分利用条件间的内在联系是解题的必经之路.审视条件要充分挖掘每一个条件的内涵和隐含信息,发掘条件的内在联系.典例(本题满分 12 分)△ABC 的内角 A,B,C 的对边分别为 a,b,c.已知△ABC 的面积为.(1)求 sin Bsin C;(2)若 6cos Bcos C=1,a=3,求△ABC 的周长.审题路线(1)→acsin B=→csin B=――→sin Csin B=→结论.(2) →cos Bcos C→sin Bsin C→cos(B+C)→求 B+C 和 A 的值,再由 S△ABC=→bcsin A=――→bc 的值――→b+c 的值→周长.标准答案阅卷现场(1)由题设得 acsin B=,①即 c sin B = 变角.②由正弦定理得 sin C sin B = 变角.③故 sin Bsin C=.④(2)由题设及(1)得 cos Bcos C-sin Bsin C=-,⑤即 cos ( B + C ) =- 变式.所以 B+C=,故 A=.⑥由题设得 bc sin A = 变式,⑦即 bc=8.⑧由余弦定理得 b2+c2-bc=9,第(1)问第(2)问得分点①②③④⑤⑥⑦⑧⑨⑩21211111116 分6 分第(1)问踩点得分说明① 写出 acsin B=得 2 分,如果没有记 0 分.② 正确变形,得出 csin B=得 1 分,越过此步不扣分.③ 正确写出 sin Csin B=得 2 分.④ 正确叙述结论得 1 分.第(2)问踩点得分说明⑤ 写出 cos Bcos C-sin Bsin C=-得 1 分.⑥ 正确求出 A 得 1 分.⑦ 正确写出 bcsinA=得 1 分.⑧ 求出 bc 的值,正确得 1 分,错误不得分.即(b+c)2-3bc=9,得 b+c=.⑨故△ABC 的周长为 3+.⑩⑨ 通过变形得出 b+c=得 1 分.⑩ 正确写出答案得 1 分.