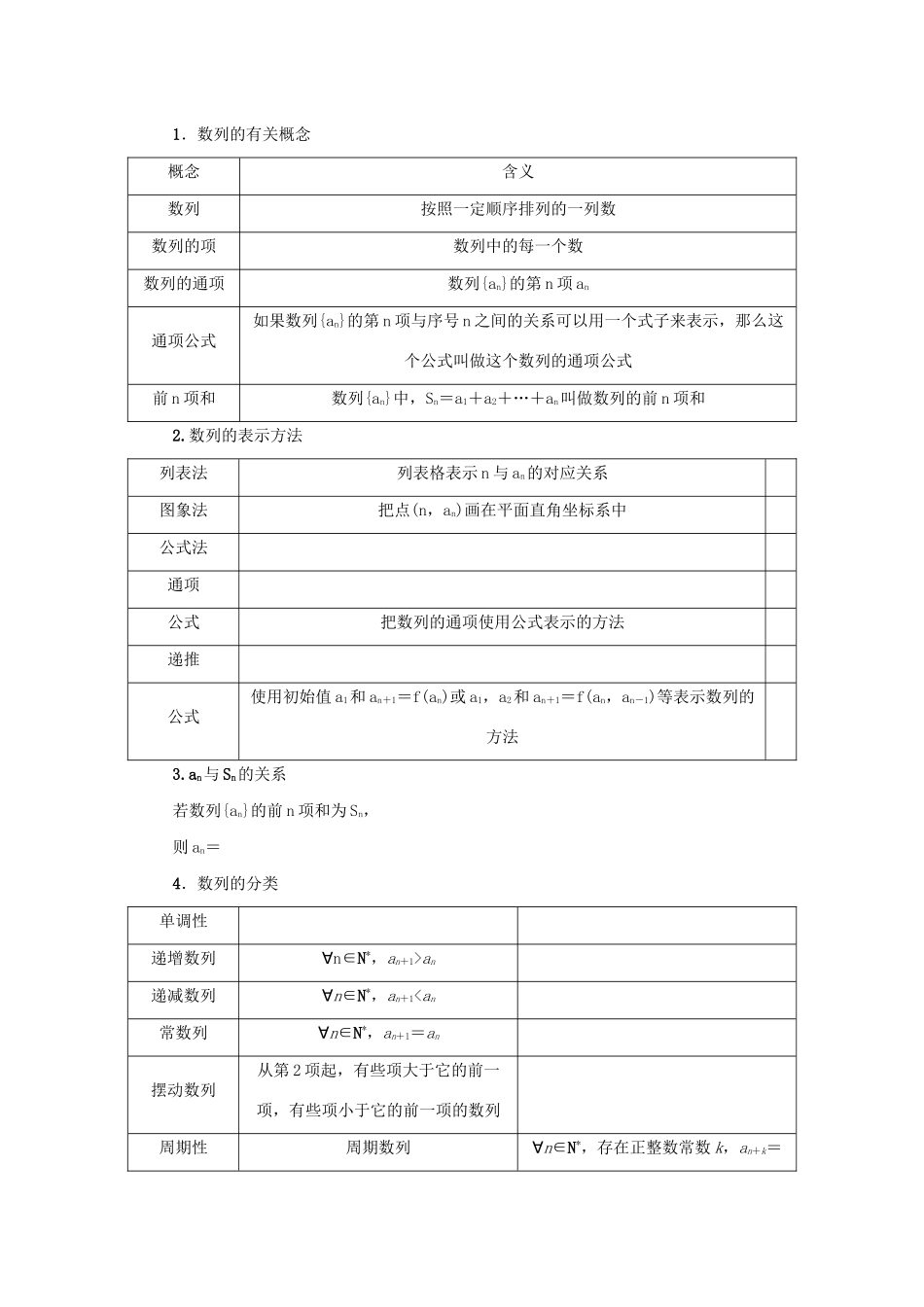
第 6 章 数 列[知识体系 p85]第 31 讲 数列的概念与通项公式【课程要求】1.了解数列的概念和几种简单的表示方法(列表、图象、通项公式).2.了解数列是自变量为正整数的一类函数.3.会利用已知数列的通项公式或递推关系式求数列的某项.4.会用数列的递推关系求其通项公式.对应学生用书 p85【基础检测】 1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)相同的一组数按不同顺序排列时都表示同一个数列.( )(2)所有数列的第 n 项都能使用公式表达.( )(3)根据数列的前几项归纳出数列的通项公式可能不止一个.( )(4)1,1,1,1,…,不能构成一个数列.( )(5)任何一个数列不是递增数列,就是递减数列.( )(6)如果数列{an}的前 n 项和为 Sn,则对∀n∈N*,都有 an+1=Sn+1-Sn.( )[答案] (1)× (2)× (3)√ (4)× (5)× (6)√2.[必修 5p33A 组 T4]在数列{an}中,a1=1,an=1+(n≥2),则 a5等于( )A.B.C.D.[解析]a2=1+=2,a3=1+=,a4=1+=3,a5=1+=.[答案]D3.[必修 5p33A 组 T5]根据下面的图形及相应的点数,写出点数构成的数列的一个通项公式 an=________.[答案]5n-44.数列{an}中,an=-n2+11n(n∈N*),则此数列最大项的值是________.[解析]an=-n2+11n=-+, n∈N*,∴当 n=5 或 n=6 时,an取最大值 30.[答案]305.已知 an=n2-λn,且对于任意的 n∈N*,数列{an}是递增数列,则实数 λ 的取值范围是________.[解析]因为{an}是递增数列,所以对任意的 n∈N*,都有 an+1>an,即(n+1)2-λ(n+1)>n2-λn,整理,得 2n+1-λ>0,即 λ<(2n+1).(*)因为 n≥1,所以 2n+1≥3,要使不等式(*)恒成立,只需 λ<3.[答案] (-∞,3)6.已知数列{an}的前 n 项和 Sn=n2+1,则 an=________.[解析]当 n=1 时,a1=S1=2,当 n≥2 时,an=Sn-Sn-1=n2+1-[(n-1)2+1]=2n-1,故 an=[答案]【知识要点】1.数列的有关概念概念含义数列按照一定顺序排列的一列数数列的项数列中的每一个数数列的通项数列{an}的第 n 项 an通项公式如果数列{an}的第 n 项与序号 n 之间的关系可以用一个式子来表示,那么这个公式叫做这个数列的通项公式前 n 项和数列{an}中,Sn=a1+a2+…+an叫做数列的前 n 项和2.数列的表示方法列表法列表格表示 n 与 an的对应关系图象法把点(n,an)画在平面直角坐标系中公式法通项公式把数列的通项使用...