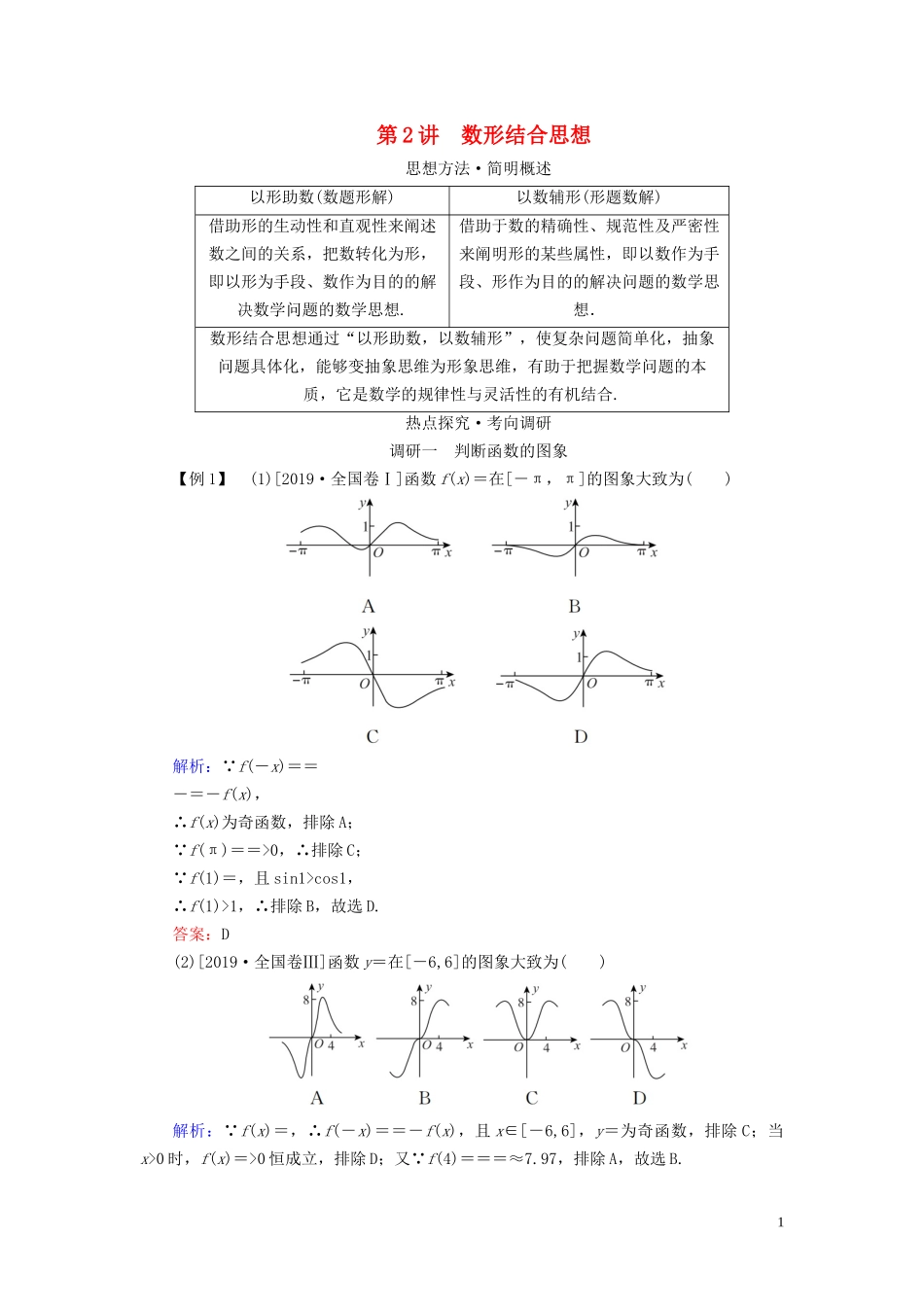
第 2 讲 数形结合思想思想方法·简明概述以形助数(数题形解)以数辅形(形题数解)借助形的生动性和直观性来阐述数之间的关系,把数转化为形,即以形为手段、数作为目的的解决数学问题的数学思想.借助于数的精确性、规范性及严密性来阐明形的某些属性,即以数作为手段、形作为目的的解决问题的数学思想.数形结合思想通过“以形助数,以数辅形”,使复杂问题简单化,抽象问题具体化,能够变抽象思维为形象思维,有助于把握数学问题的本质,它是数学的规律性与灵活性的有机结合.热点探究·考向调研调研一 判断函数的图象【例 1】 (1)[2019·全国卷Ⅰ]函数 f(x)=在[-π,π]的图象大致为( )解析: f(-x)==-=-f(x),∴f(x)为奇函数,排除 A; f(π)==>0,∴排除 C; f(1)=,且 sin1>cos1,∴f(1)>1,∴排除 B,故选 D.答案:D(2)[2019·全国卷Ⅲ]函数 y=在[-6,6]的图象大致为( )解析: f(x)=,∴f(-x)==-f(x),且 x∈[-6,6],y=为奇函数,排除 C;当x>0 时,f(x)=>0 恒成立,排除 D;又 f(4)===≈7.97,排除 A,故选 B.1答案:B(3)[2019·浙江卷]在同一直角坐标系中,函数 y=,y=loga(a>0,且 a≠1)的图象可能是( )解析:若 0
1,则 y=是减函数,y=loga是增函数,结合选项可知,没有符合的图象,故选 D.答案:D方法点睛函数图象的判断可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的奇偶性,判断图象的对称性.(3)从函数的特征点,排除不合要求的图象.(4)从函数的单调性,判断图象的变化趋势.调研二 函数的零点与方程的根【例 2】 (1)[2019·浙江卷]设 a,b∈R,f(x)=若函数 y=f(x)-ax-b 恰有 3 个零点,则( )A.a<-1,b<0 B.a<-1,b>0C.a>-1,b<0D.a>-1,b>0解析:记 g(x)=f(x)-ax-b.当 x<0 时,g(x)=(1-a)x-b,最多有 1 个零点.当x≥0 时,g(x)=x3-(a+1)x2-b,g′(x)=x2-(a+1)x=x[x-(a+1)].若 a+1≤0,即a≤-1,则 g′(x)≥0,g(x)在(0,+∞)上单调递增,所以 g(x)在[0,+∞)上最多有 1个零点,因此 g(x)在 R 上最多有 2 个零点,不合题意,所以 a>-1.当 x∈[0,a+1)时,g′(x)<0,g(x)单调递减;当 x∈(a+1,+∞)时,g′(x)>0,g(x)单调递增,所以当 ...