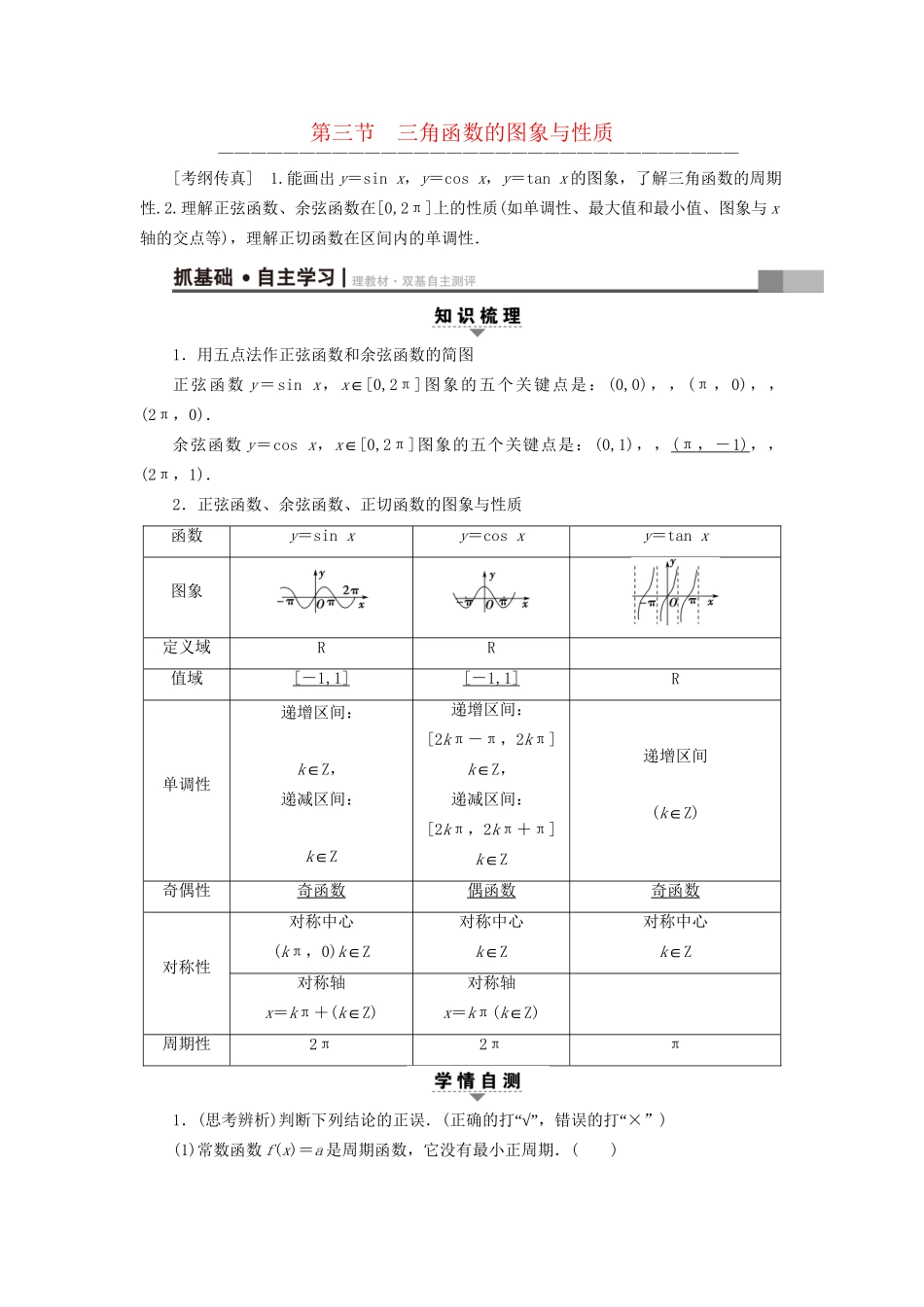
第三节三角函数的图象与性质————————————————————————————————[考纲传真]1.能画出y=sinx,y=cosx,y=tanx的图象,了解三角函数的周期性.2.理解正弦函数、余弦函数在[0,2π]上的性质(如单调性、最大值和最小值、图象与x轴的交点等),理解正切函数在区间内的单调性.1.用五点法作正弦函数和余弦函数的简图正弦函数y=sinx,x∈[0,2π]图象的五个关键点是:(0,0),,(π,0),,(2π,0).余弦函数y=cosx,x∈[0,2π]图象的五个关键点是:(0,1),,(π,-1),,(2π,1).2.正弦函数、余弦函数、正切函数的图象与性质函数y=sinxy=cosxy=tanx图象定义域RR值域[-1,1][-1,1]R单调性递增区间:k∈Z,递减区间:k∈Z递增区间:[2kπ-π,2kπ]k∈Z,递减区间:[2kπ,2kπ+π]k∈Z递增区间(k∈Z)奇偶性奇函数偶函数奇函数对称性对称中心(kπ,0)k∈Z对称中心k∈Z对称中心k∈Z对称轴x=kπ+(k∈Z)对称轴x=kπ(k∈Z)周期性2π2ππ1.(思考辨析)判断下列结论的正误.(“√”“正确的打,错误的打×”)(1)常数函数f(x)=a是周期函数,它没有最小正周期.()(2)函数y=sinx的图象关于点(kπ,0)(k∈Z)中心对称.()(3)正切函数y=tanx在定义域内是增函数.()(4)y=sin|x|是偶函数.()[答案](1)√(2)√(3)×(4)√2.(2017·云南二次统一检测)函数f(x)=cos的图象关于()A.原点对称B.y轴对称C.直线x=对称D.直线x=-对称A[函数f(x)=cos=-sin2x是奇函数,则图象关于原点对称,故选A.]3.函数y=tan2x的定义域是()A.B.C.D.D[由2x≠kπ+,k∈Z,得x≠+,k∈Z,∴y=tan2x的定义域为.]4.(2017·长沙模拟(一))函数y=sin,x∈[-2π,2π]的单调递增区间是()A.B.和C.D.C[令z=x+,函数y=sinz的单调递增区间为(k∈Z),由2kπ≤-x≤+2kπ+得4kπ≤-x≤4kπ+,而x∈[-2π,2π],故其单调递增区间是,故选C.]5.(教材改编)函数f(x)=4-2cosx的最小值是________,取得最小值时,x的取值集合为________.2{x|x=6kπ,k∈Z}[f(x)min=4-2=2,此时,x=2kπ(k∈Z),x=6kπ(k∈Z),所以x的取值集合为{x|x=6kπ,k∈Z}.]三角函数的定义域与值域(1)(2016·全国卷Ⅱ)函数f(x)=cos2x+6cos的最大值为()A.4B.5C.6D.7(2)函数y=lg(sin2x)+的定义域为________.(1)B(2)∪[(1) f(x)=cos2x+6cos=cos2x+6sinx=1-2sin2x+6sinx=-22+,又sinx∈[-1,1],∴当sinx=1时,f(x)取得最大值5.故选B.(2)由得∴-3≤x<-或0<x<,∴函数y=lg(sin2x)+的定义域为∪.][规律方法]1.三角函数定义域的求法求三角函数定义域实际上是构造简单的三角不等式(组),常借助三角函数线或三角函数图象来求解.2.求三角函数最值或值域的常用方法(1)直接法:直接利用sinx和cosx的值域求解.(2)化一法:把所给三角函数化为y=Asin(ωx+φ)+k的形式,由正弦函数单调性写出函数的值域.(3)换元法:把sinx,cosx,sinxcosx或sinx±cosx换成t,转化为二次函数求解.[变式训练1](1)已知函数y=2cosx的定义域为,值域为[a,b],则b-a的值是()A.2B.3C.+2D.2-(2)求函数y=cos2x+sinx的最大值与最小值.【导学号:31222113】(1)B[ x∈,∴cosx∈,故y=2cosx的值域为[-2,1],∴b-a=3.](2)令t=sinx, |x|≤,∴t∈,3分∴y=-t2+t+1=-2+,∴当t=时,ymax=,当t=-时,ymin=,7分∴函数y=cos2x+sinx的最大值为,最小值为.12分三角函数的单调性(1)(2017·洛阳模拟)已知ω>0,函数f(x)=sin在上单调递减,则ω的取值范围是()A.B.C.D.(0,2](2)函数f(x)=sin的单调减区间为________.(1)A(2)(k∈Z)[(1)由<x<π得ω+<ωx+<πω+,由题意知⊆,≤所以解得ω≤.(2)由已知函数为y=-sin,欲求函数的单调减区间,只需求y=sin的单调增区间即可.由2kπ≤-2x≤-2kπ+,k∈Z,得kπ≤-x≤kπ+,k∈Z.故所求函数的单调减区间为(k∈Z).][规律方法]1.求三角函数单调区间的两种方法(1)求函数的单调区间应遵循简化原则,将解析式先化简,并注意复合函数单调性规律“”同增异减.(2)求形如y=Asin(ωx+φ)(ω>0)“的单调区间时,要视...