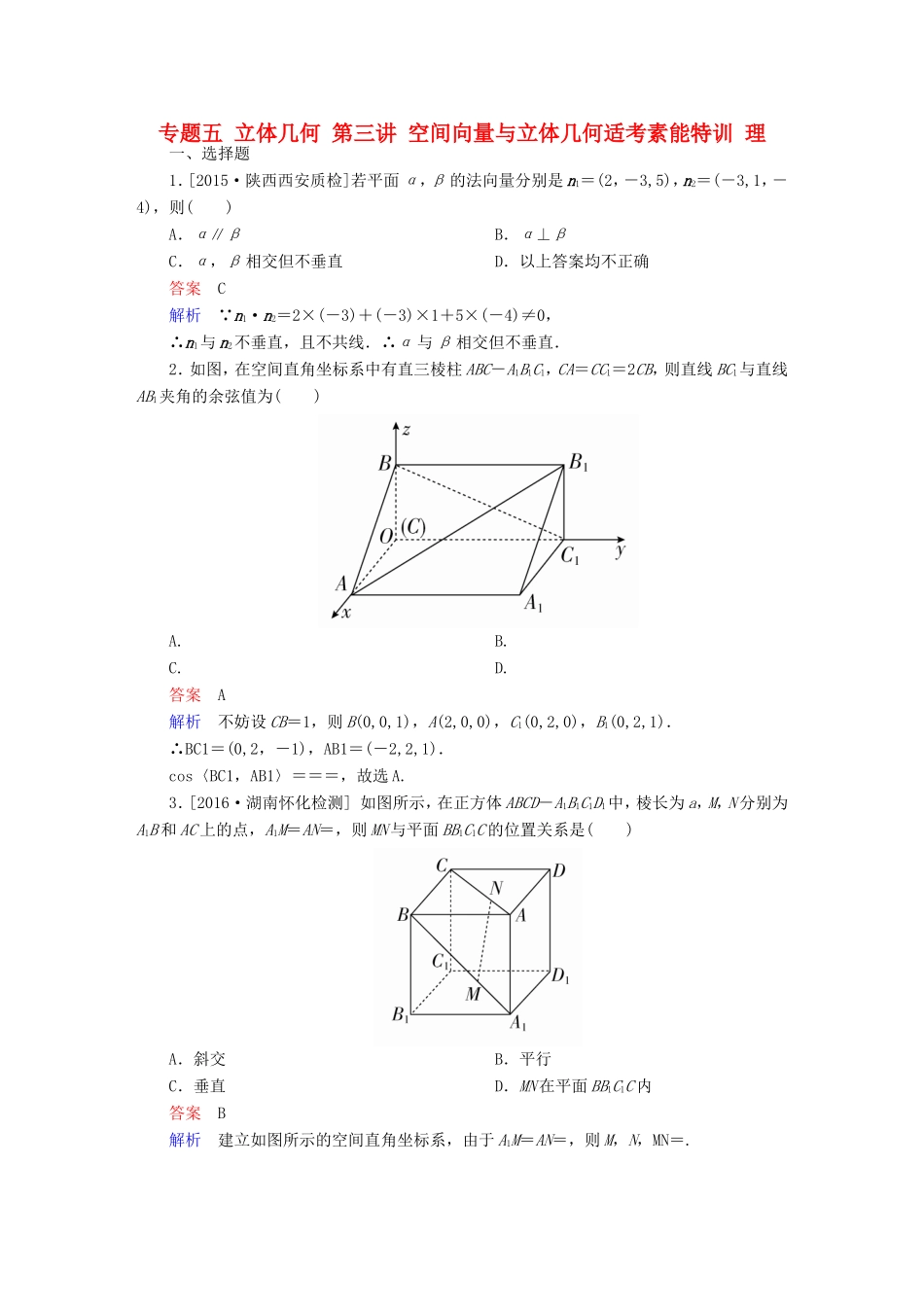
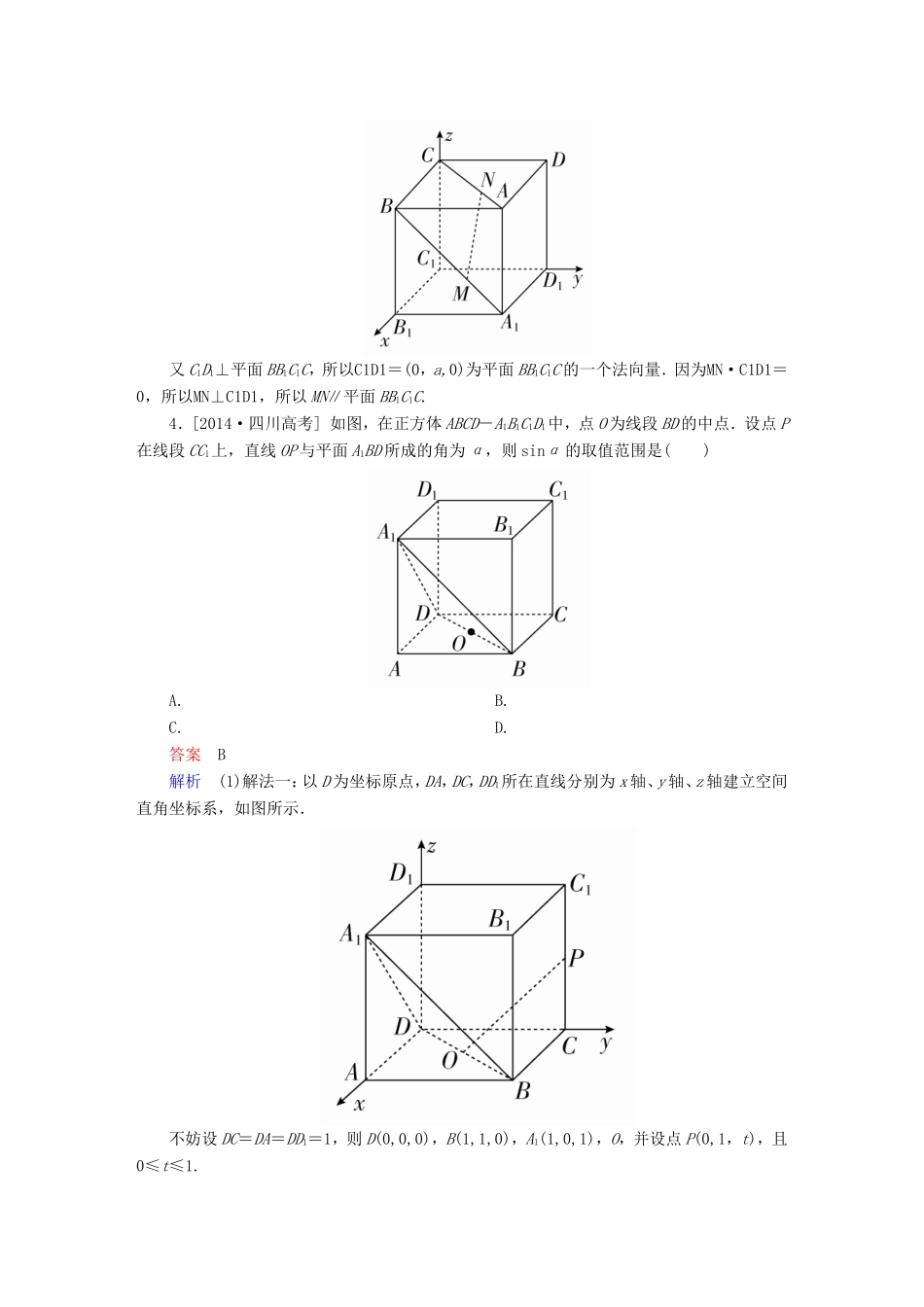
专题五立体几何第三讲空间向量与立体几何适考素能特训理一、选择题1.[2015·陕西西安质检]若平面α,β的法向量分别是n1=(2,-3,5),n2=(-3,1,-4),则()A.α∥βB.α⊥βC.α,β相交但不垂直D.以上答案均不正确答案C解析 n1·n2=2×(-3)+(-3)×1+5×(-4)≠0,∴n1与n2不垂直,且不共线.∴α与β相交但不垂直.2.如图,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为()A.B.C.D.答案A解析不妨设CB=1,则B(0,0,1),A(2,0,0),C1(0,2,0),B1(0,2,1).∴BC1=(0,2,-1),AB1=(-2,2,1).cos〈BC1,AB1〉===,故选A.3.[2016·湖南怀化检测]如图所示,在正方体ABCD-A1B1C1D1中,棱长为a,M,N分别为A1B和AC上的点,A1M=AN=,则MN与平面BB1C1C的位置关系是()A.斜交B.平行C.垂直D.MN在平面BB1C1C内答案B解析建立如图所示的空间直角坐标系,由于A1M=AN=,则M,N,MN=.又C1D1⊥平面BB1C1C,所以C1D1=(0,a,0)为平面BB1C1C的一个法向量.因为MN·C1D1=0,所以MN⊥C1D1,所以MN∥平面BB1C1C.4.[2014·四川高考]如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点.设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是()A.B.C.D.答案B解析(1)解法一:以D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示.不妨设DC=DA=DD1=1,则D(0,0,0),B(1,1,0),A1(1,0,1),O,并设点P(0,1,t),且0≤t≤1.则OP=,A1D=(-1,0,-1),A1B=(0,1,-1).设平面A1BD的法向量为n=(x0,y0,z0),则有即取x0=1,y0=-1,z0=-1,∴n=(1,-1,-1).∴sinα=|cos〈OP,n〉|=(0≤t≤1),∴sin2α=,0≤t≤1.令f(t)=,0≤t≤1.则f′(t)==-,可知当t∈时,f′(t)>0;当t∈时,f′(t)≤0.又 f(0)=,f=1,f(1)=,∴fmax(t)=f=1,fmin(t)=f(0)=.∴sinα的最大值为1,最小值为.∴sinα的取值范围为,故选B.解法二:易证AC1⊥平面A1BD,当点P在线段CC1上从C运动到C1时,直线OP与平面A1BD所成的角α的变化情况:∠AOA1→→∠C1OA1(点P为线段CC1的中点时,α=).由于sin∠AOA1=,sin∠C1OA1=>,sin=1,所以sinα的取值范围是,故选B.二、填空题5.[2016·江苏苏州二模]已知正方形ABCD的边长为4,CG⊥平面ABCD,CG=2,E,F分别是AB,AD的中点,则点C到平面GEF的距离为________.答案解析建立如图所示的空间直角坐标系Cxyz,相关各点的坐标为G(0,0,2),F(4,2,0),E(2,4,0),C(0,0,0),则CG=(0,0,2),GF=(4,2,-2),GE=(2,4,-2).设平面GEF的法向量为n=(x,y,z),由得平面GEF是一个法向量为n=(1,1,3),所以点C到平面GEF的距离d==.三、解答题6.[2015·甘肃天水一模]如图,在四棱锥S-ABCD中,底面ABCD为梯形,AD∥BC,AD⊥平面SCD,AD=DC=2,BC=1,SD=2,∠SDC=120°.(1)求SC与平面SAB所成角的正弦值;(2)求平面SAD与平面SAB所成的锐二面角的余弦值.解如图,在平面SCD中,过点D作DC的垂线交SC于E,以D为原点,DA,DC,DE所在直线分别为x轴,y轴,z轴,建立空间直角坐标系.则有D(0,0,0),S(0,-1,),A(2,0,0),C(0,2,0),B(1,2,0).(1)设平面SAB的法向量为n=(x,y,z), AB=(-1,2,0),AS=(-2,-1,),AB·n=0,AS·n=0,∴取y=,得n=(2,,5).又SC=(0,3,-),设SC与平面SAB所成角为θ,则sinθ=|cos〈SC,n〉|==,故SC与平面SAB所成角的正弦值为.(2)设平面SAD的法向量为m=(a,b,c), DA=(2,0,0),DS=(0,-1,),则有取b=,得m=(0,,1).∴cos〈n,m〉===,故平面SAD与平面SAB所成的锐二面角的余弦值是.7.[2014·全国卷Ⅰ]如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.(1)证明:AC=AB1;(2)若AC⊥AB1,∠CBB1=60°,AB=BC,求二面角A-A1B1-C1的余弦值.解(1)证明:连接BC1,交B1C于点O,连接AO.因为侧面BB1C1C为菱形,所以B1C⊥BC1,且O为B1C及BC1的中点.又AB⊥B1C,所以B1C⊥平面ABO.由于AO⊂平面ABO,故B1C⊥AO.又B1O=CO,故AC=AB1.(2)因为AC⊥AB1,且O为B1C的中点,所以AO=CO....