高考数学二轮复习 专题25 审题技能训练（含解析）试题VIP免费

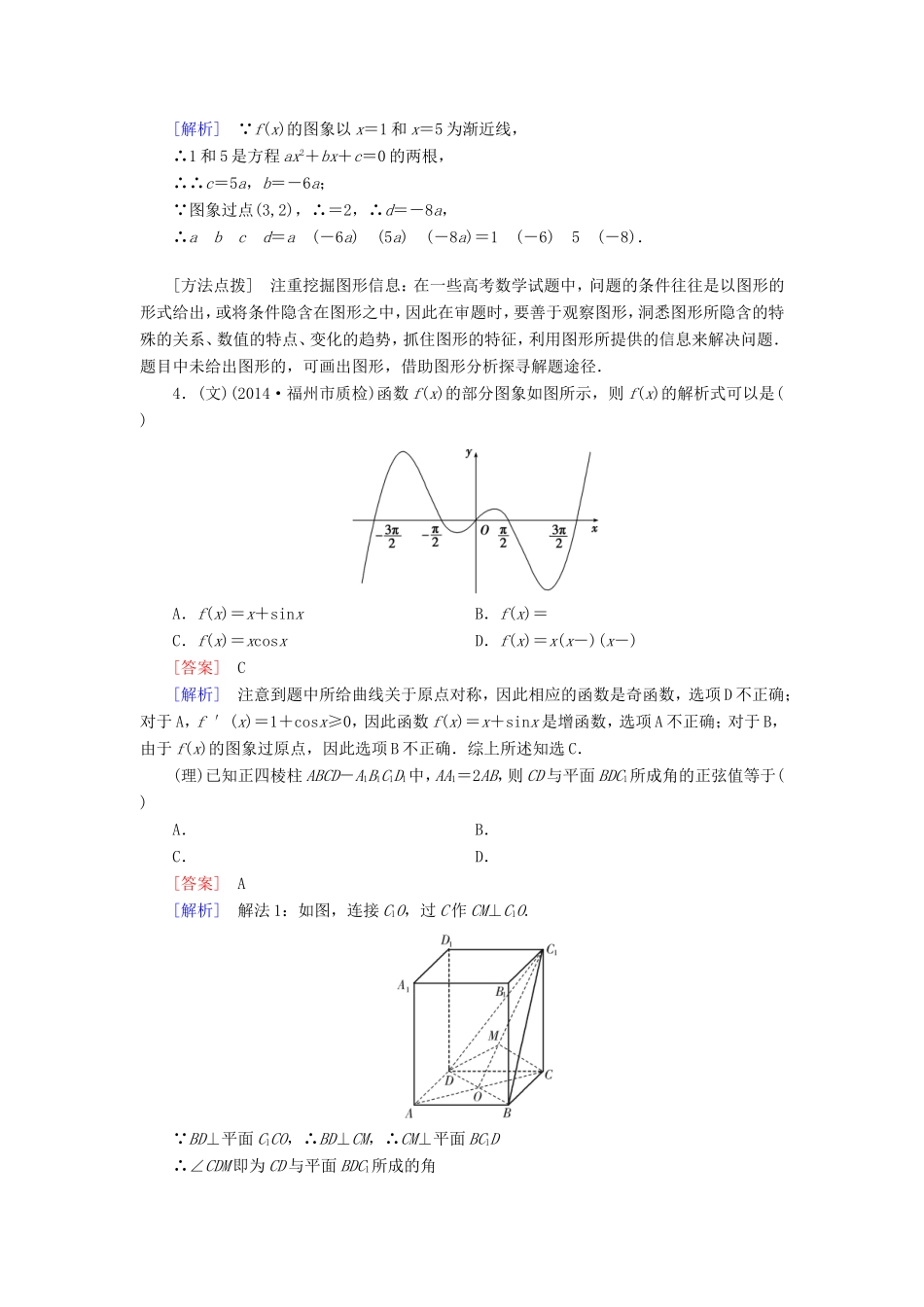
一、选择题1．已知向量a、b的夹角为60°，且|a|＝2，|b|＝1，则向量a与向量a＋2b的夹角等于()A．150°B．90°C．60°D．30°[答案]D[审题要点]弄清问题、熟悉问题和转化问题要求向量的夹角，可由cosθ＝求解，这是求向量夹角的常用方法，→由已知可求解a·(a＋2b)＝a2＋2a·b的值．→由已知可求|a＋2b|2＝a2＋4a·b＋4b2的值，进而可求|a＋2b|的值．→由上述步骤可求得cosθ＝的值．[解析]|a＋2b|2＝4＋4＋4a·b＝8＋8cos60°＝12，∴|a＋2b|＝2，记向量a与向量a＋2b的夹角为θ，则a·(a＋2b)＝|a|·|a＋2b|·cosθ＝2×2cosθ＝4cosθ，又a·(a＋2b)＝a2＋2a·b＝4＋4cos60°＝6，∴4cosθ＝6，cosθ＝，又θ∈[0，π]，∴θ＝，故选D．2．(文)对于函数f(x)＝asinx＋bx＋c(其中，a，b∈R，c∈Z)，选取a，b，c的一组值计算f(1)和f(－1)，所得出的正确结果一定不可能是()A．4和6B．3和1C．2和4D．1和2[答案]D[审题要点]仔细观察会发现f(x)的表达式中“asinx＋bx”有其特殊性，即g(x)＝asinx＋bx为奇函数，这是本题审题第一关键要素，其实从f(1)与f(－1)的提示，也应考虑是否具有奇偶性可用，由此可知f(1)＋f(－1)＝2c；再注意观察细节可以发现c∈Z，从而2c为偶数．[解析]令g(x)＝asinx＋bx，则g(x)为奇函数，∴g(－1)＝－g(1)，∴f(x)＝g(x)＋c.∴f(1)＋f(－1)＝g(1)＋c＋g(－1)＋c＝2c， c∈Z，∴2c为偶数， 1＋2＝3不是偶数，∴1和2一定不是f(1)与f(－1)的一组值，故选D．(理)已知函数f(x)是定义在R上的偶函数，且在区间[0，＋∞)上单调递增．若实数a满足f(log2a)＋f(loga)≤2f(1)，则a的取值范围是()A．[1,2]B．(0，]C．[，2]D．(0,2][答案]C[审题要点]求a的取值范围，需解给出的不等式，条件中的单调递增为解不等式时脱去函数符号“f”所备，f(x)为偶函数，为化不等式为f(x1)≤f(x2)型而准备．解题思路步骤为：――→――→――→[解析]因为loga＝－log2a且f(－x)＝f(x)，则f(log2a)＋f(loga)≤2f(1)⇒f(log2a)＋f(－log2a)≤2f(1)⇒f(log2a)≤f(1)．又f(log2a)＝f(|log2a|)且f(x)在[0，＋∞)上单调递增，∴|log2a|≤1⇒－1≤log2a≤1，解得≤a≤2，选C．[方法点拨]注意发掘隐含条件有的题目条件不甚明显，而寓于概念、存于性质或含于图中，审题时，注意深入挖掘这些隐含条件和信息，就可避免因忽视隐含条件而出现的错误．3．(文)(2014·浙江理，3)某几何体的三视图(单位：cm)如图所示，则此几何体的表面积是()A．90cm2B．129cm2C．132cm2D．138cm2[答案]D[审题要点]――→――→――→――――――――――――→表面积[解析]由三视图知该几何体是一个直三棱柱与长方体的组合体，长方体长、宽、高分别为4cm,6cm,3cm，直棱柱高为3cm，底面为直角三角形，两直角边长为3cm、4cm，∴几何体的表面积为S＝2×4×6＋2×3×4＋3×6＋3×3＋3×4＋3×5＋2××3×4＝138cm2，选D．(理)若函数f(x)＝(a、b、c、d∈R)的图象如图所示，则abcd＝()A．165(－8)B．1(－6)5(－8)C．1(－6)58D．1658[答案]B[解析] f(x)的图象以x＝1和x＝5为渐近线，∴1和5是方程ax2＋bx＋c＝0的两根，∴∴c＝5a，b＝－6a； 图象过点(3,2)，∴＝2，∴d＝－8a，∴abcd＝a(－6a)(5a)(－8a)＝1(－6)5(－8)．[方法点拨]注重挖掘图形信息：在一些高考数学试题中，问题的条件往往是以图形的形式给出，或将条件隐含在图形之中，因此在审题时，要善于观察图形，洞悉图形所隐含的特殊的关系、数值的特点、变化的趋势，抓住图形的特征，利用图形所提供的信息来解决问题．题目中未给出图形的，可画出图形，借助图形分析探寻解题途径．4．(文)(2014·福州市质检)函数f(x)的部分图象如图所示，则f(x)的解析式可以是()A．f(x)＝x＋sinxB．f(x)＝C．f(x)＝xcosxD．f(x)＝x(x－)(x－)[答案]C[解析]注意到题中所给曲线关于原点对称，因此相应的函数是奇函数，选项D不正确；对于A，f′(x)＝1＋cosx≥0，因此函数f(x)＝x＋sinx是增函数，选项A不正确；对于B，由于f(x)的图象过原点，因此选项B不正确．综上所述知选C．(理)已知正四棱柱ABCD－A1B1C1D1中，AA1＝2AB，则CD与平面BDC1...