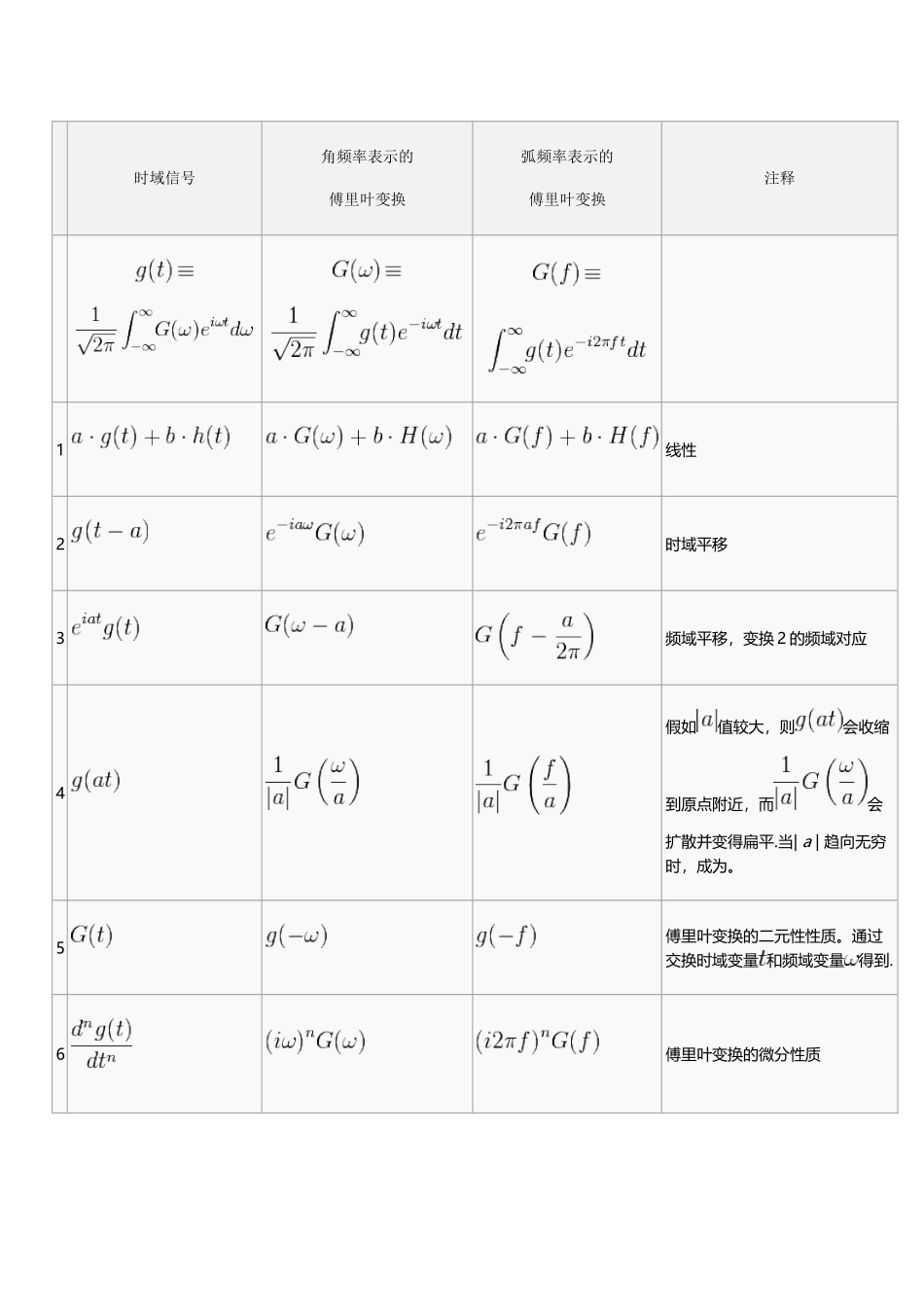
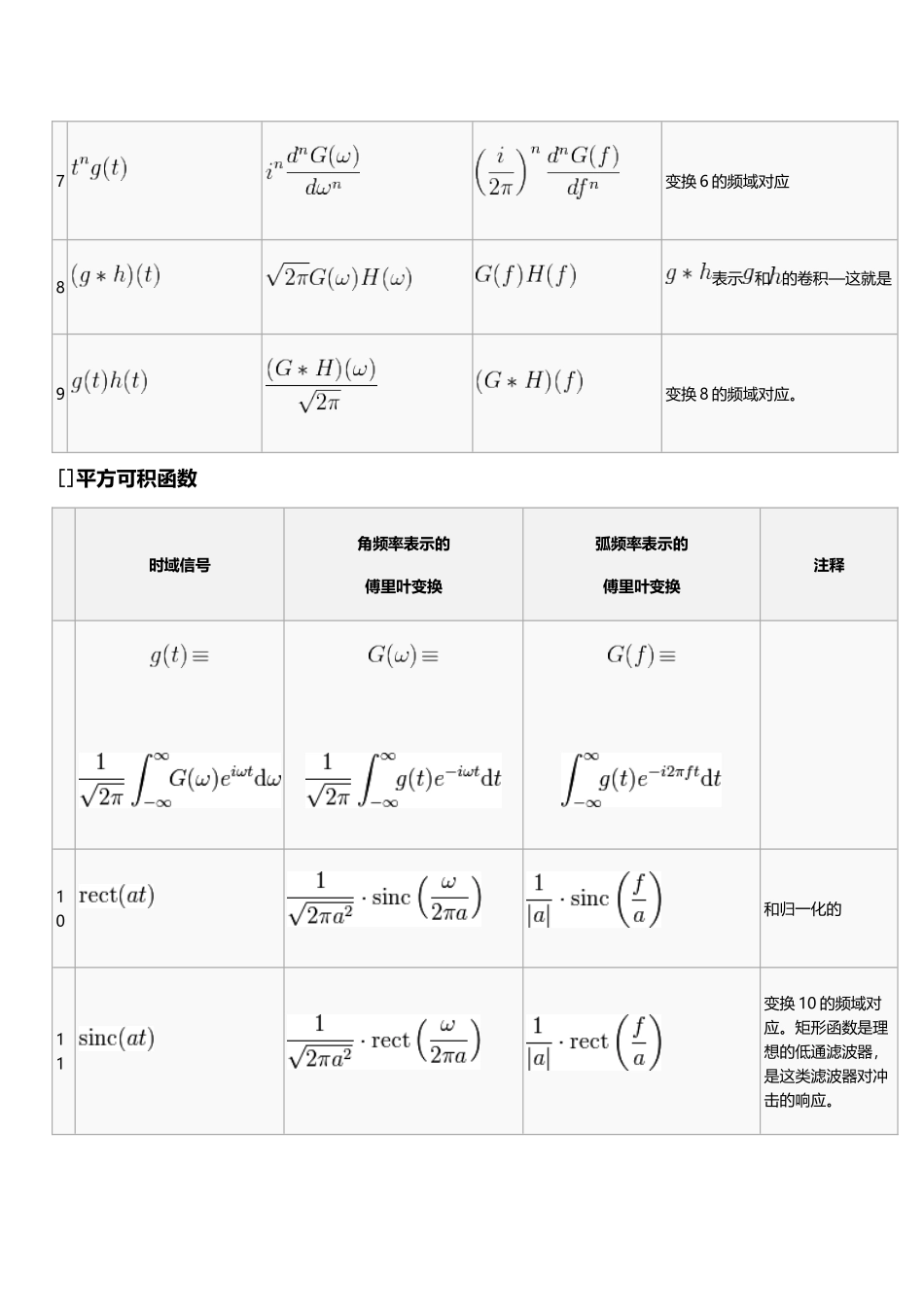
常用傅里叶变换(6 页)Good is good, but better carries it.精益求精,善益求善。时域信号角频率表示的傅里叶变换弧频率表示的傅里叶变换注释1线性2时域平移3频域平移,变换 2 的频域对应4假如值较大,则会收缩到原点附近,而会扩散并变得扁平.当| a | 趋向无穷时,成为。5傅里叶变换的二元性性质。通过交换时域变量 和频域变量得到.6傅里叶变换的微分性质7变换 6 的频域对应8表示 和 的卷积—这就是9变换 8 的频域对应。[]平方可积函数时域信号角频率表示的傅里叶变换弧频率表示的傅里叶变换注释10和归一化的11变换 10 的频域对应。矩形函数是理想的低通滤波器,是这类滤波器对冲击的响应。12tri 是13变换 12 的频域对应14exp( − αt2)的傅里叶变换是他本身.只有当 Re(α) > 0时,这是可积的。15领域应用较多161718a>019变换本身就是一个公式20J0(t) 是。21上一个变换的推广形式; Tn(t) 是。22 Un (t)是。[]分布时域信号角频率表示的傅里叶变换弧频率表示的傅里叶变换注释23δ(ω)代表分布.这个变换展示了狄拉克 δ 函数的重要性:该函数是常函数的傅立叶变换24变换 23 的频域对应25由变换 3 和 24 得到.26由变换 1 和 25 得到,应用了: cos(at) = (eiat + e − iat) / 2.27由变换 1 和 25 得到28这里, n 是一个.δ(n)(ω)是狄拉克 δ 函数分布的 n 阶微分。这个变换是根据变换 7 和 24 得到的。将此变换与 1 结合使用,我们可以变换所有。29此处 sgn(ω)为;注意此变换与变换 7 和 24 是一致的.30变换 29 的推广.31变换 29 的频域对应.32此处 u(t)是;此变换根据变换 1 和 31 得到.33u(t)是,且 a > 0.34——有助于解释或理解从连续到的转变.[]二元函数时域信号角频率表示的傅里叶变换弧频率表示的傅里叶变换注释两个函数都是高斯函数,而且可能都没有单位体积.此圆有单位半径,假如把 circ(t)认作阶梯函数u(1-t); Airy 分布用 J1 (1 阶)表达; fr是频率矢量的量值{fx,fy}.三元函数时域信号角频率表示的傅里叶变弧频率表示的傅里叶变换注释换此球有单位半径;fr是频率矢量的量值{fx,fy,fz}.}((<¥***…¥/'';]~,`}《;:&(|—?!【》