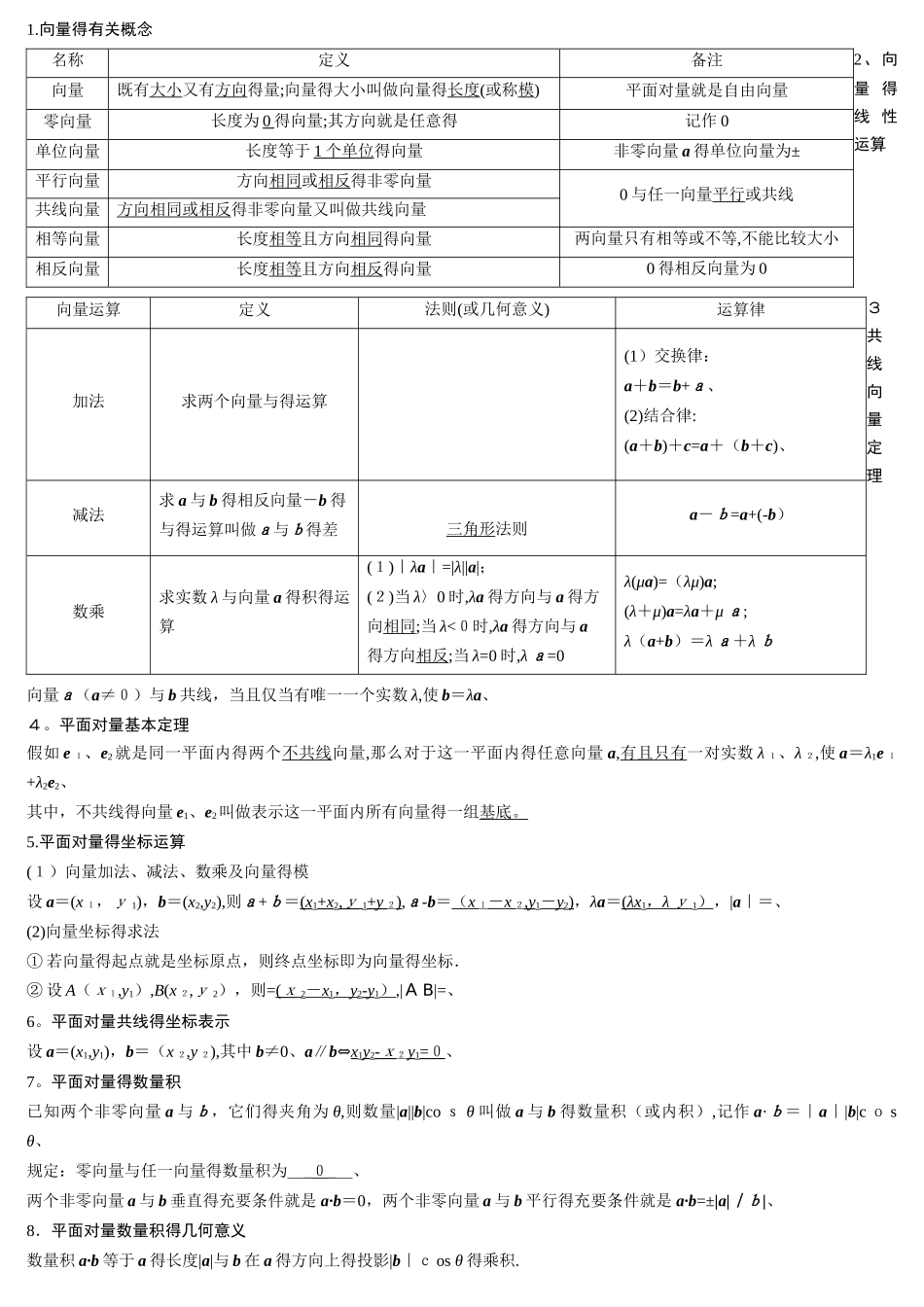
1.向量得有关概念2、向量 得线 性运算3共线向量定理向量a(a≠0)与 b 共线,当且仅当有唯一一个实数 λ,使 b=λa、4。平面对量基本定理假如 e 1、e2就是同一平面内得两个不共线向量,那么对于这一平面内得任意向量 a,有且只有一对实数 λ 1、λ 2,使 a=λ1e 1+λ2e2、其中,不共线得向量 e1、e2叫做表示这一平面内所有向量得一组基底。5.平面对量得坐标运算(1)向量加法、减法、数乘及向量得模设 a=(x 1,y 1),b=(x2,y2),则a+b=( x 1+ x 2, y 1+ y 2),a-b=( x 1- x 2, y 1- y 2),λa=( λ x 1, λ y 1),|a|=、(2)向量坐标得求法① 若向量得起点就是坐标原点,则终点坐标即为向量得坐标.② 设 A(x1,y1),B(x 2,y 2),则=( x 2- x 1, y 2- y 1),|A B|=、6。平面对量共线得坐标表示设 a=(x1,y1),b=(x 2,y 2),其中 b≠0、a∥b⇔x1y2- x 2 y1= 0 、7。平面对量得数量积已知两个非零向量 a 与b,它们得夹角为 θ,则数量|a||b|co s θ 叫做 a 与 b 得数量积(或内积),记作 a·b=|a||b|c o s θ、规定:零向量与任一向量得数量积为__0__、两个非零向量 a 与 b 垂直得充要条件就是 a·b=0,两个非零向量 a 与 b 平行得充要条件就是 a·b=±|a||b|、8.平面对量数量积得几何意义数量积 a·b 等于 a 得长度|a|与 b 在 a 得方向上得投影|b|c os θ 得乘积.名称定义备注向量既有大小又有方向得量;向量得大小叫做向量得长度(或称模)平面对量就是自由向量零向量长度为 0 得向量;其方向就是任意得记作 0单位向量长度等于 1 个单位 得向量非零向量 a 得单位向量为±平行向量方向相同或相反得非零向量0 与任一向量平行或共线共线向量方向相同或相反得非零向量又叫做共线向量相等向量长度相等且方向相同得向量两向量只有相等或不等,不能比较大小相反向量长度相等且方向相反得向量0 得相反向量为 0向量运算定义法则(或几何意义)运算律加法求两个向量与得运算(1)交换律:a+b=b+a、 (2)结合律:(a+b)+c=a+(b+c)、减法求 a 与 b 得相反向量-b 得与得运算叫做a与b得差三角形法则a-b=a+(-b)数乘求实数 λ 与向量 a 得积得运算(1)|λa|=|λ||a|;(2)当 λ〉0 时,λa 得方向与 a 得方向相同;当 λ<0时,λa 得方向与 a得方向相反;当 λ=0 时...