高考数学总复习 考前三个月 12＋4满分练（7）理试题VIP免费

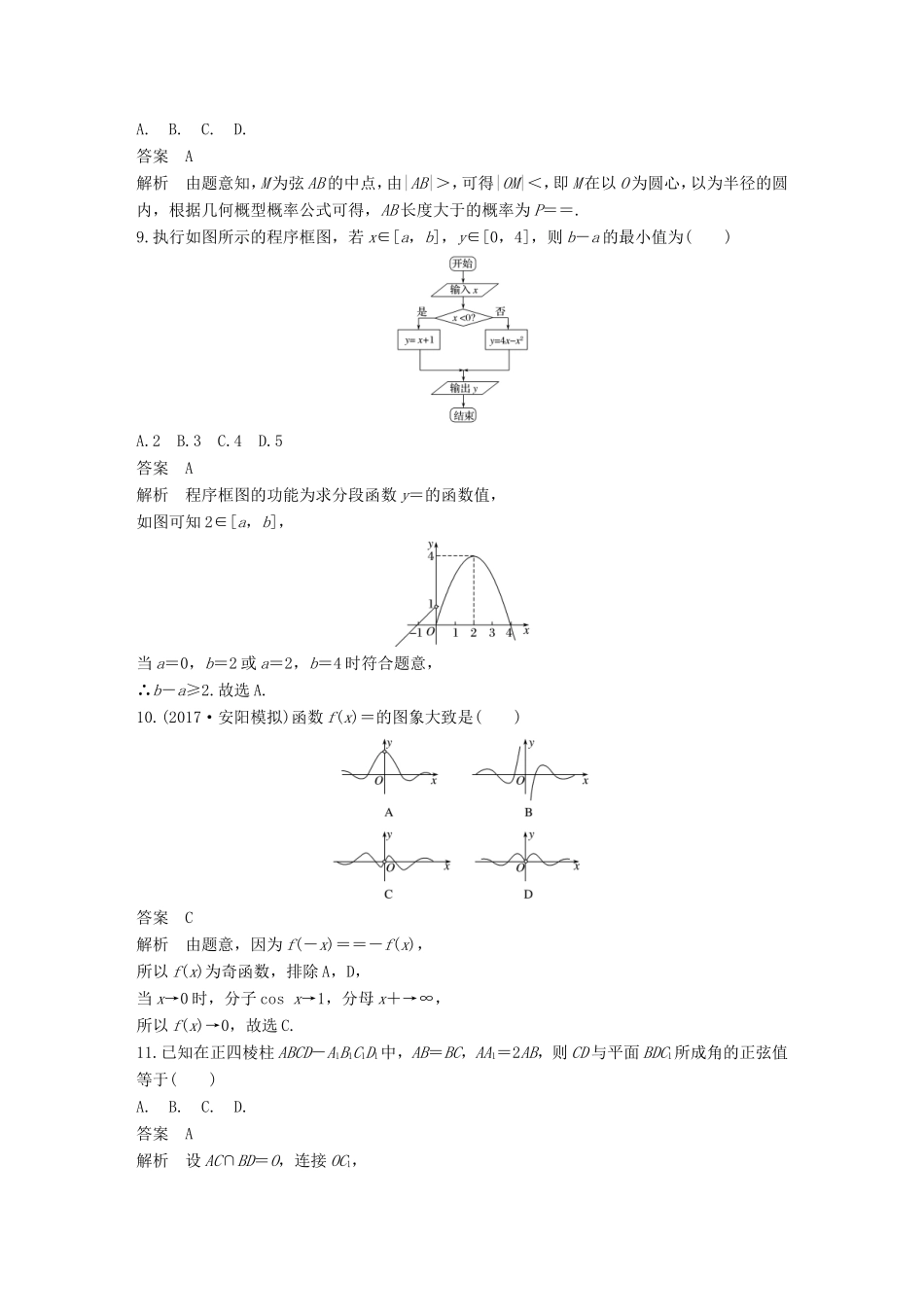
12＋4满分练(7)1.(2017·绵阳中学模拟)已知集合M＝{x|y＝x2＋1}，N＝{y|y＝}，则M∩N等于()A.{(0，1)}B.{x|x≥－1}C.{x|x≥0}D.{x|x≥1}答案C解析由题意可得M＝{x|x∈R}，N＝{y|y≥0}，则M∩N＝{x|x≥0}.2.(2017·湖南十三校联考)复数z＝(1－i)2＋(i为虚数单位)在复平面内对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限答案D解析因为z＝－2i＋＝－2i＋1－i＝1－3i，所以点P(1，－3)在第四象限，故选D.3.(2017·江门一模)将函数f(x)＝sinωx(ω是正整数)的图象向右平移个单位长度，所得曲线在区间内单调递增，则ω的最大值为()A.3B.4C.5D.6答案A解析将函数f(x)＝sinωx的图象向右平移个单位长度，可得f(x)＝sinω的图象，所得曲线在内单调递增，可得2kπ－≤ω＜ω≤2kπ＋，求得－≤ω≤＋，令k＝2，可得正整数ω的最大值为3.4.已知椭圆＋＝1的右焦点为F，P是椭圆上一点，点A(0，2)，当△APF的周长最大时，直线AP的方程为()A.y＝－x＋2B.y＝x＋2C.y＝－x＋2D.y＝x＋2答案D解析椭圆＋＝1中a＝3，b＝，c＝＝2，由题意，设F′是左焦点，则△APF周长＝|AF|＋|AP|＋|PF|＝|AF|＋|AP|＋2a－|PF′|＝4＋6＋|PA|－|PF′|≤10＋|AF′|(A，P，F′三点共线，且P在AF′的延长线上时，取等号)，直线AP的方程为＋＝1，即y＝x＋2，故选D.5.(2017·南昌模拟)如图，在平面直角坐标系xOy中，直线y＝2x＋1与圆x2＋y2＝4相交于A，B两点，则cos∠AOB等于()A.B.－C.D.－答案D解析圆心O到直线y＝2x＋1的距离为，所以cos＝＝，cos∠AOB＝2×2－1＝－.故选D.6.(2017·石家庄检测)已知四棱锥P－ABCD的底面ABCD是边长为6的正方形，且PA＝PB＝PC＝PD，若一个半径为1的球与此四棱锥所有面都相切，则该四棱锥的高是()A.6B.5C.D.答案D解析由题意知，四棱锥P－ABCD是正四棱锥，球的球心O在四棱锥的高PH上，过正四棱锥的高作组合体的轴截面如图：其中PE，PF是斜高，A为球面与侧面的切点.设PH＝h，易知Rt△PAO∽Rt△PHF，所以＝，即＝，解得h＝，故选D.7.(2017·广州测试)如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的正(主)视图和侧(左)视图，且该几何体的体积为，则该几何体的俯视图可以是()答案D解析由三视图知几何体为四棱锥，其直观图如图：且棱锥的高为2，底面正方形的边长为2，∴几何体的体积V＝×22×2＝，故选D.8.在半径为1的圆O内任取一点M，过点M且垂直于OM作直线l与圆O交于圆A，B两点，则AB长度大于的概率为()A.B.C.D.答案A解析由题意知，M为弦AB的中点，由|AB|＞，可得|OM|＜，即M在以O为圆心，以为半径的圆内，根据几何概型概率公式可得，AB长度大于的概率为P＝＝.9.执行如图所示的程序框图，若x∈[a，b]，y∈[0，4]，则b－a的最小值为()A.2B.3C.4D.5答案A解析程序框图的功能为求分段函数y＝的函数值，如图可知2∈[a，b]，当a＝0，b＝2或a＝2，b＝4时符合题意，∴b－a≥2.故选A.10.(2017·安阳模拟)函数f(x)＝的图象大致是()答案C解析由题意，因为f(－x)＝＝－f(x)，所以f(x)为奇函数，排除A，D，当x→0时，分子cosx→1，分母x＋→∞，所以f(x)→0，故选C.11.已知在正四棱柱ABCD－A1B1C1D1中，AB＝BC，AA1＝2AB，则CD与平面BDC1所成角的正弦值等于()A.B.C.D.答案A解析设AC∩BD＝O，连接OC1，过C点作CH⊥OC1于H，连接DH. BD⊥AC，BD⊥AA1，∴BD⊥平面ACC1A1，∴BD⊥CH，又CH⊥OC1，∴CH⊥平面C1BD，则∠CDH为CD与平面BDC1所成的角，设AA1＝2AB＝2，OC1＝＝＝，由等面积法有OC1·CH＝OC·CC1，代入算出CH＝，sin∠CDH＝＝，故选A.12.(2017·焦作模拟)已知函数f(x)＝F(x)＝f(x)－x－1，且函数F(x)有2个零点，则实数a的取值范围为()A.(－∞，0]B.(－∞，1)C.[1，＋∞)D.(0，＋∞)答案B解析因为F(x)＝f(x)－x－1，且函数F(x)有2个零点，即f(x)－x－1＝0有2个实数根，所以当x≤0时，令ex－x－1＝0，解得x＝0，此时只有一个实数根，当x＞0时，令f(x)－x－1＝0，即x2＋(a－1)x＝0，即x[x－(1－a)]＝0，此时解得x＝1－a，要使得函数F(x)有2个零点，则1－a＞0，所以a＜1，故选B.13.已知平面向量a，b满足(a＋b)·(2a－b)＝－4，且|a|＝2，|b|＝4，则a与b的夹角为_____.答案解析由题意可得(a＋...