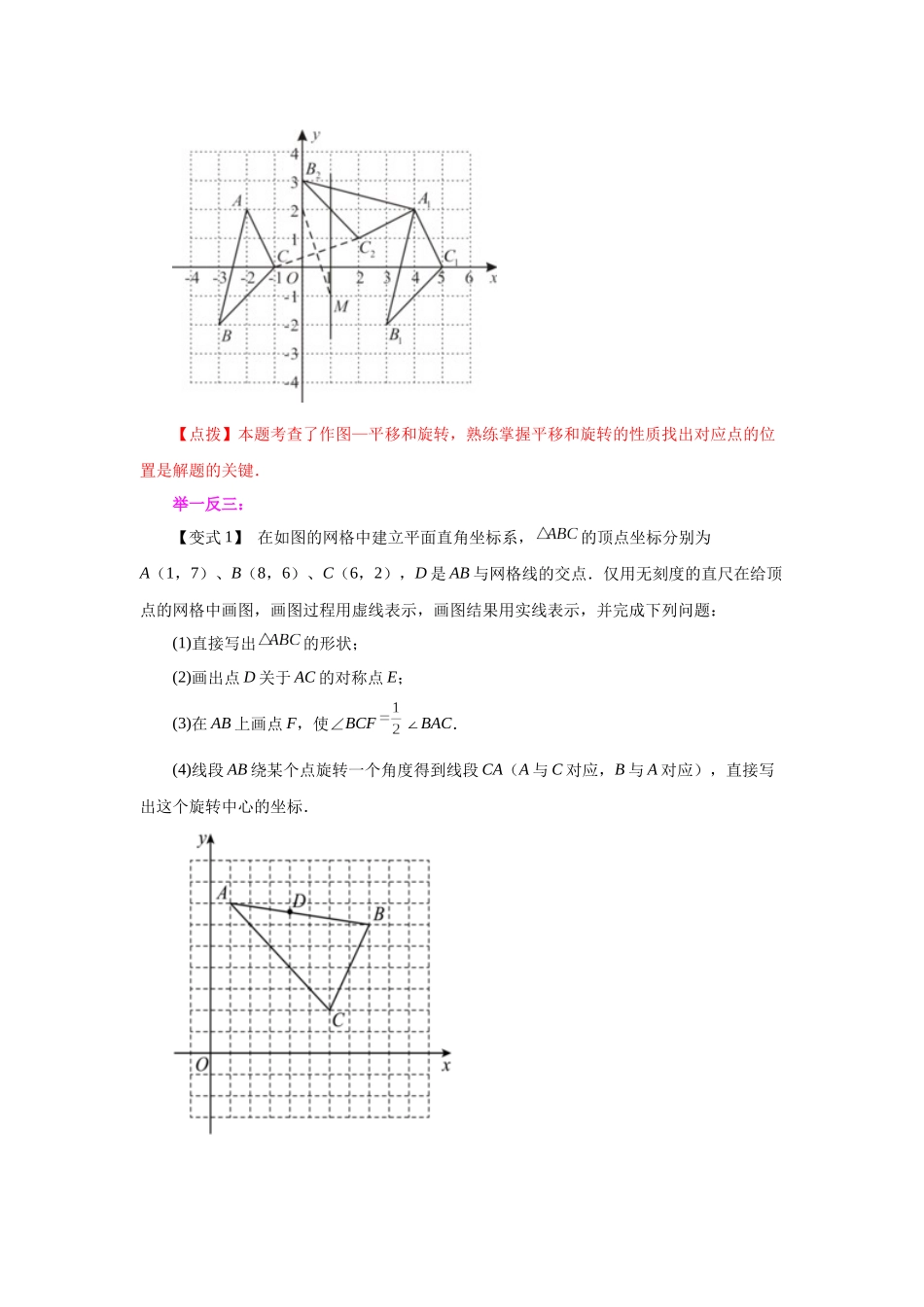
专题 23.1 图形的旋转(知识讲解)【学习目标】1、掌握旋转的概念,探索它的基本性质,理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质;2、能够按要求作出简单平面图形旋转后的图形,并能利用旋转进行简单的图案设计.【要点梳理】要点一、旋转的概念把一个图形绕着某一点 O 转动一个角度的图形变换叫做旋转..点 O 叫做旋转中心,转动的角叫做旋转角(如∠AO A′),如果图形上的点 A 经过旋转变为点 A′,那么,这两个点叫做这个旋转的对应点.特别说明:旋转的三个要素:旋转中心、旋转方向和旋转角度.要点二、旋转的性质(1)对应点到旋转中心的距离相等(OA= OA′); (2)对应点与旋转中心所连线段的夹角等于旋转角; (3)旋转前、后的图形全等(△ABC≌△).特别说明:图形绕某一点旋转,既可以按顺时针旋转也可以按逆时针旋转. 要点三、旋转的作图在画旋转图形时,首先确定旋转中心,其次确定图形的关键点,再将这些关键点沿指定的方向旋转指定的角度,然后连接对应的部分,形成相应的图形.特别说明:作图的步骤:(1)连接图形中的每一个关键点与旋转中心;(2)把连线按要求(顺时针或逆时针)绕旋转中心旋转一定的角度(旋转角); (3)在角的一边上截取关键点到旋转中心的距离,得到各点的对应点; (4)连接所得到的各对应点.【典型例题】类型一、旋转中心、旋转角、对应点1.在平面直角坐标系 xOy 中,的顶点坐标分别是,,.(1)按要求画出图形:① 将向右平移 6 个单位得到;② 再将绕点顺时针旋转 90°得到;(2)如果将(1)中得到的看成是由经过以某一点 M 为旋转中心旋转一次得到的,请写出 M 的坐标.【答案】(1)① 见分析;②见分析;(2)M(1,-1)【分析】(1)①根据平移的性质得出、、的位置,顺次连接即可;② 根据旋转的性质得出、的位置,顺次连接即可;(2)连接 CC2,AA1,线段 CC2,AA1的垂直平分线的交点即为 M 点的位置,作出 M点写出坐标即可.(1)解:①如图,即为所求;② 如图,即为所求;(2)解:连接 CC2,AA1,线段 CC2,AA1的垂直平分线的交点即为 M 点的位置,由图可知,M 的坐标为(1,-1).【点拨】本题考查了作图—平移和旋转,熟练掌握平移和旋转的性质找出对应点的位置是解题的关键.举一反三:【变式 1】 在如图的网格中建立平面直角坐标系,的顶点坐标分别为A(1,7)、B(8,6)、C(6,2),D 是 AB 与网格线的交点.仅用无刻度的直尺在...