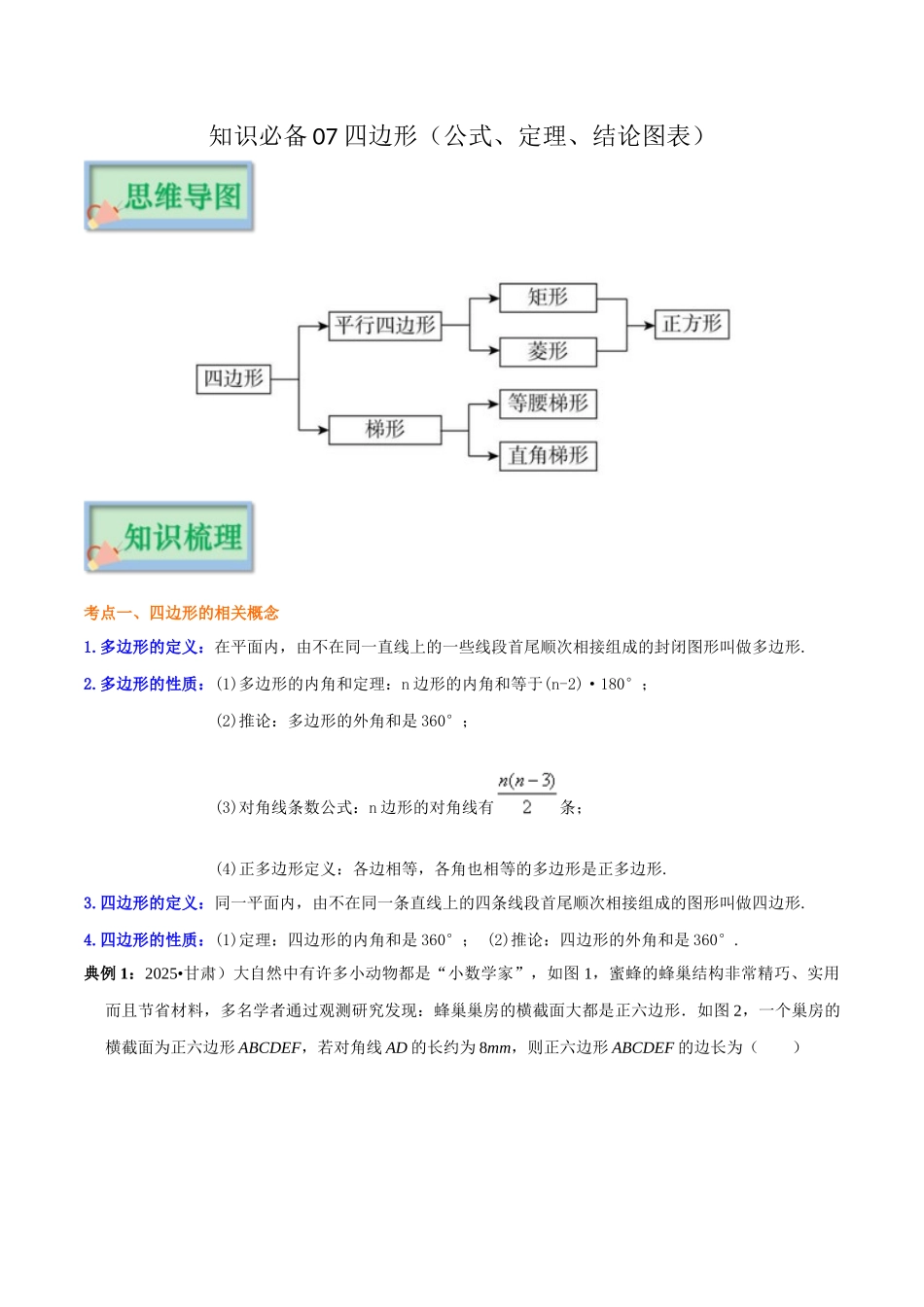
知识必备 07 四边形(公式、定理、结论图表)考点一、四边形的相关概念1.多边形的定义:在平面内,由不在同一直线上的一些线段首尾顺次相接组成的封闭图形叫做多边形.2.多边形的性质:(1)多边形的内角和定理:n 边形的内角和等于(n-2)·180°; (2)推论:多边形的外角和是 360°; (3)对角线条数公式:n 边形的对角线有条; (4)正多边形定义:各边相等,各角也相等的多边形是正多边形.3.四边形的定义:同一平面内,由不在同一条直线上的四条线段首尾顺次相接组成的图形叫做四边形.4.四边形的性质:(1)定理:四边形的内角和是 360°; (2)推论:四边形的外角和是 360°.典例 1:2025•甘肃)大自然中有许多小动物都是“小数学家”,如图 1,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图 2,一个巢房的横截面为正六边形 ABCDEF,若对角线 AD 的长约为 8mm,则正六边形 ABCDEF 的边长为( )A.2mmB.2mmC.2mmD.4mm【分析】根据正六边形的性质和题目中的数据,可以求得正六边形 ABCDEF 的边长.【解答】解:连接 BE,CF,BE、CF 交于点 O,如右图所示, 六边形 ABCDEF 是正六边形,AD 的长约为 8mm,∴∠AOF=60°,OA=OD=OF,OA 和 OD 约为 4mm,∴AF 约为 4mm,故选:D.【点评】本题考查多边形的对角线,解答本题的关键是明确正六边形的特点.典例 2:(2025•柳州)如图,四边形 ABCD 的内角和等于( )A.180°B.270°C.360°D.540°【分析】根据四边形的内角和等于 360°解答即可.【解答】解:四边形 ABCD 的内角和为 360°.故选:C.【点评】本题考查了四边形的内角和,四边形的内角和等于 360°.考点二、特殊的四边形1.平行四边形及特殊的平行四边形的性质2. 平行四边形及特殊的平行四边形的判定【要点诠释】面积公式:S 菱形 =12 ab=ch.(a、b 为菱形的对角线 ,c 为菱形的边长 ,h 为 c 边上的高)S 平行四边形 =ah. a 为平行四边形的边,h 为 a 上的高)典例 3:(2025•朝阳)将一个三角尺按如图所示的方式放置在一张平行四边形的纸片上,∠EFG=90°,∠EGF=60°,∠AEF=50°,则∠EGC 的度数为( )A.100°B.80°C.70°D.60°【分析】由平行四边形的性质可得 AB∥DC,再根据三角形内角和定理,即可得到∠GEF 的度数,依据平行线的性质,即可得到∠EGC 的度数.【解答】解: 四...