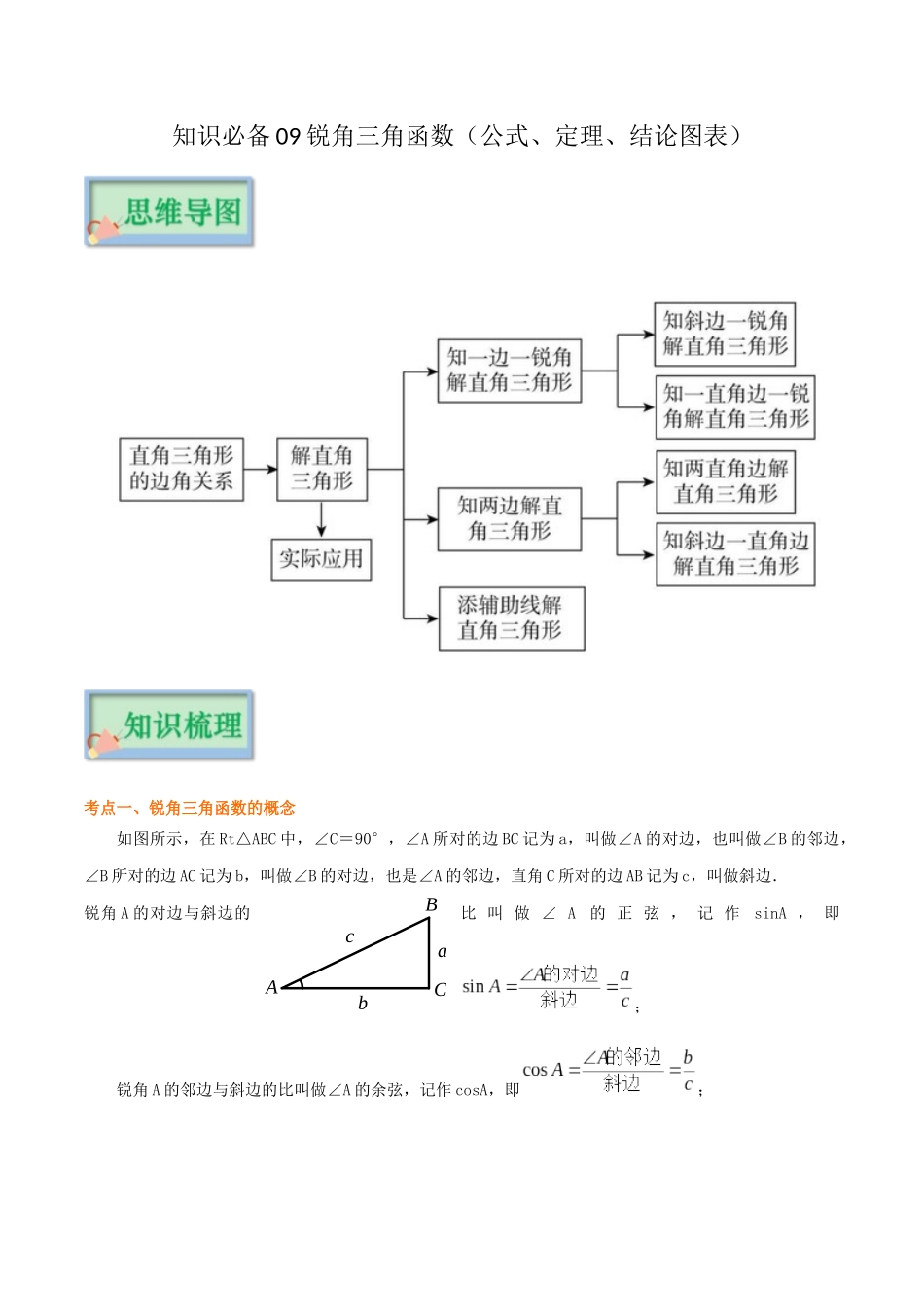
知识必备 09 锐角三角函数(公式、定理、结论图表)考点一、锐角三角函数的概念如图所示,在 Rt△ABC 中,∠C=90°,∠A 所对的边 BC 记为 a,叫做∠A 的对边,也叫做∠B 的邻边,∠B 所对的边 AC 记为 b,叫做∠B 的对边,也是∠A 的邻边,直角 C 所对的边 AB 记为 c,叫做斜边.锐角 A 的对边与斜边的比 叫 做 ∠ A的 正 弦 , 记 作sinA , 即;锐角 A 的邻边与斜边的比叫做∠A 的余弦,记作 cosA,即;ABCabc锐角 A 的对边与邻边的比叫做∠A 的正切,记作 tanA,即.同理;;.要点诠释: (1)正弦、余弦、正切函数是在直角三角形中定义的,反映了直角三角形边与角的关系,是两条线段的比值.角的度数确定时,其比值不变,角的度数变化时,比值也随之变化. (2)sinA,cosA,tanA 分别是一个完整的数学符号,是一个整体,不能写成,,,不能理解成 sin 与∠A,cos 与∠A,tan 与∠A 的乘积.书写时习惯上省略∠A 的角的记号“∠”,但对三个大写字母表示成的角(如∠AEF),其正切应写成“tanAEF”∠,不能写成“tanAEF”;另外,、、常写成、、. (3)任何一个锐角都有相应的锐角三角函数值,不因这个角不在某个三角形中而不存在. (4)由锐角三角函数的定义知:当角度在 0°<∠A<90°之间变化时,,,tanA>0.典例 1:(2025•扬州)在△ABC 中,∠C=90°,a、b、c 分别为∠A、∠B、∠C 的对边,若 b2=ac,则sinA 的值为 . .【分析】根据勾股定理和锐角三角函数的定义解答即可.【解答】解:在△ABC 中,∠C=90°,∴c2=a2+b2, b2=ac,∴c2=a2+ac,等式两边同时除以 ac 得:=+1,令=x,则有=x+1,∴x2+x1﹣ =0,解得:x1=,x2=(舍去),当 x=时,x≠0,∴x=是原分式方程的解,sin∴A==.故答案为:.【点评】本题主要考查了锐角三角函数,熟练掌握勾股定理和锐角三角函数的定义是解答本题的关键.考点二、特殊角的三角函数值 利用三角函数的定义,可求出 0°、30°、45°、60°、90°角的各三角函数值,归纳如下: 要点诠释: (1)通过该表可以方便地知道 0°、30°、45°、60°、90°角的各三角函数值,它的另一个应用就是:如果知道了一个锐角的三角函数值,就可以求出这个锐角的度数,例如:若,则锐角. (2)仔细研究表中数值的规律会发现: 、、、、的值依次为 0、、、、1,而、、、、的值的顺序正好相反,、、的值依次增大,其变化规律可...