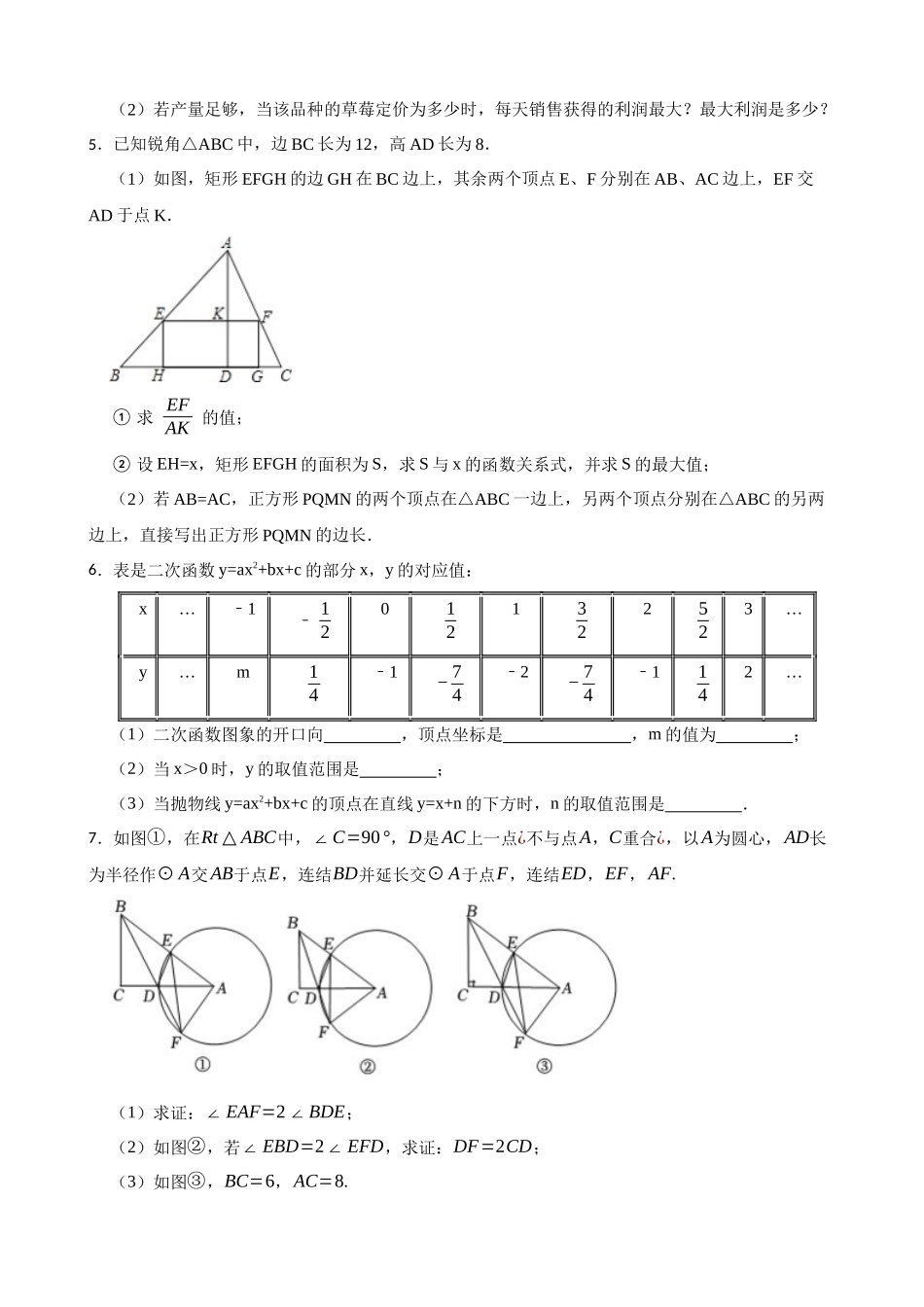
2026 年中考数学高频考点突破-二次函数的最值问题一、综合题1.某工艺品厂生产一种汽车装饰品,每件生产成本为 20 元,销售价格在 30 元至 80 元之间(含 30元和 80 元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计 50 万元,其销售量y(万个)与销售价格 x(元/个)的函数关系如图所示.(1)当 30≤x≤60 时,求 y 与 x 的函数关系式;(2)求出该厂生产销售这种产品的纯利润 w(万元)与销售价格 x(元/个)的函数关系式;(3)销售价格应定为多少元时,获得利润最大,最大利润是多少?2.在平面直角坐标系中,设二次函数 y1=ax2+2x+c,y2=cx2+2x+a(a,c 是实数且 ac≠0).(1)若函数 y1的对称轴是直线 x=1 且函数 y1的图象经过点(0,3),求函数 y1的表达式.(2)在(1)的条件下,当﹣1≤x≤0 时,y2的取值范围.(3)设函数 y1和函数 y2的最大值分别为 m 和 n.若 m+n=0,探究实数 a,c 满足的关系式.3.已知x=t2−3, y=1+t ,S=x+8 y.(1)求 S 与 t 的函数关系式;(2)当t=2时,求 S 的值;(3)求 S 的最大值或最小值.4.某地草莓已经到了收获季节,已知草莓的成本价为 10 元/千克,投入市场销售后,发现该草莓销售不会亏本,且每天销售量 y(千克)与销售单价 x(元/千克)之间的函数关系如图所示.(1)求 y 与 x 的函数关系式,并写出 x 的取值范围.(2)若产量足够,当该品种的草莓定价为多少时,每天销售获得的利润最大?最大利润是多少?5.已知锐角△ABC 中,边 BC 长为 12,高 AD 长为 8. (1)如图,矩形 EFGH 的边 GH 在 BC 边上,其余两个顶点 E、F 分别在 AB、AC 边上,EF 交AD 于点 K. ① 求 EFAK 的值;② 设 EH=x,矩形 EFGH 的面积为 S,求 S 与 x 的函数关系式,并求 S 的最大值;(2)若 AB=AC,正方形 PQMN 的两个顶点在△ABC 一边上,另两个顶点分别在△ABC 的另两边上,直接写出正方形 PQMN 的边长. 6.表是二次函数 y=ax2+bx+c 的部分 x,y 的对应值: x…1﹣ ﹣ 120121322523…y…m141﹣− 742﹣− 741﹣142…(1)二次函数图象的开口向 ,顶点坐标是 ,m 的值为 ; (2)当 x>0 时,y 的取值范围是 ; (3)当抛物线 y=ax2+bx+c 的顶点在直线 y=x+n 的下方时,n 的取值范围是 . 7.如图①,在Rt △ ABC中,∠C=90°,D是AC上一点¿...