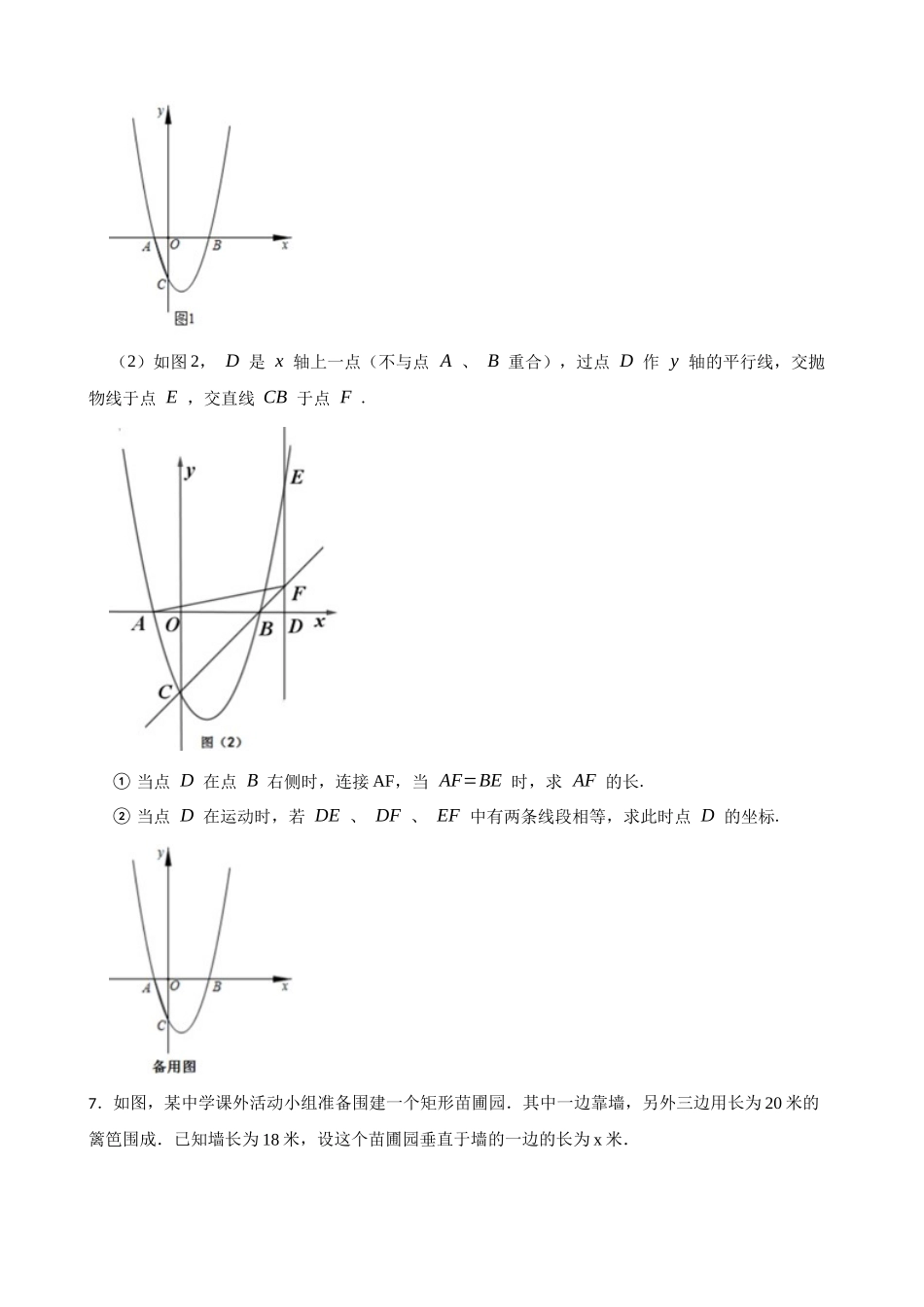
2026 年中考数学高频考点突破-二次函数与几何问题1.如图,用40 m的篙色围成一个边靠墙的矩形场地,墙长15m.垂直于墙的边长为xm.围成的矩形场地的面积为y m2.(1)求 y 与 x 的函数关系式,并写出自变量 x 的取值范围;(2)求这个矩形场地面积的最大值.2.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用 28m 长的篱笆围成一个矩形花园 ABCD(篱笆只围 AB,BC 两边),设 AB=xm. (1)若花园的面积为 192m2,求 x 的值; (2)若在 P 处有一棵树与墙 CD,AD 的距离分别是 15m 和 6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积 S 的最大值. 3.如图,一张正方形纸板的边长为 2cm,将它剪去 4 个全等的直角三角形(图中阴影部分).设AE=BF=CG=DH=xcm,四边形 EFGH 的面积为 ycm2, (1)求 y 关于 x 的函数表达式和自变量 x 的取值范围; (2)求四边形 EFGH 的面积为 3cm2时的 x 值; (3)四边形 EFGH 的面积可以为 1.5cm2吗?请说明理由. 4.某公司对办公大楼一块墙面进行如图所示的图案设计.这个图案由四个全等的直角三角形和一个小正方形拼接而成的大正方形,设小正方形的边长 m,直角三角形较短直角边长 n,且 n=m2﹣ ,大正方形的面积为 S.(1)求 S 关于 m 的函数关系式;(2)若小正方形边长不大于 3,当大正方形面积最大时,求 m 的值.5.如图所示,将抛物线 y= 12 x2沿 x 轴向右平移 2 个单位长度,再向下平移 1 个单位长度,得到新的抛物线. (1)直接写出新抛物线的解析式为 ; (2)设新抛物线交 x 轴于 A、B 两点,交 y 轴于 C,顶点为 D,作 CECD⊥交抛物线于 E,如图所示,探究如下问题:① 求点 E 的坐标;② 若一次函数 y=kx+1 的图象与抛物线存在唯一交点且交对称轴交于点 F,连接 DE,猜测直线DE 与对称轴的夹角和一次函数 y=kx+1 的图象与对称轴的夹角之间的大小关系,并证明.6.已知,在平面直角坐标系中, O 为坐标原点,抛物线 y=a x2−2ax −3a (a≠0) 分别交 x 轴于 A 、 B 两点(点 A 在点 B 的侧),与 y 轴交于点 C ,连接 AC , tan∠ ACO=13 .(1)如图 1,求 a 的值; (2)如图 2, D 是 x 轴上一点(不与点 A 、 B 重合),过点 D 作 y 轴的平行线,交抛物线于点 E ,交直线 CB 于点 F ....