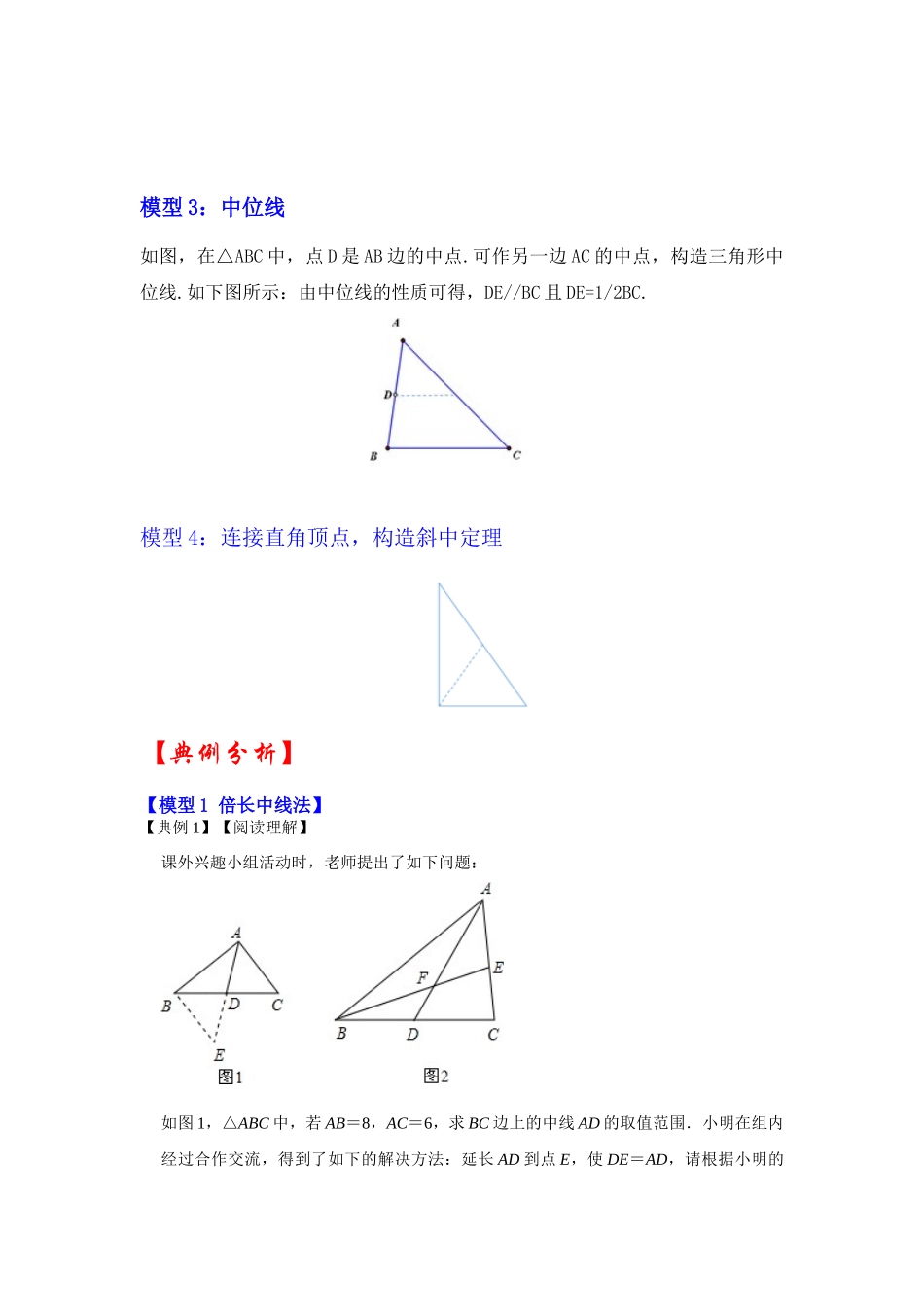
专题 02 中点四大模型在三角形中应用(知识解读)【专题说明】 线段中点是几何部分一个非常重要的概念,和后面学习的中线,中位线等概念有着密切的联系.在几何证明题中也屡次出现.那么,如果在题中遇到中点你会想到什么?等腰三角形三线合一;直角三角形斜边上的中线等于斜边的一半;还是中位线定理?今天我们重点探究“倍长中线”法以及平行线间夹中点时延长中线交平行等的应用。【方法技巧】模型 1 :倍长中线法如图,在△ABC 中,AD 是 BC 边上的中线. 当题中出现中线时,我们经常根据需要将 AD 延长,使延长部分和中线相等,这种方法叫做“倍长中线”.如下图:此时,易证△ACD≌EDB,进而得到 AC=BE 且 AC//BE. 模型 2:平行线夹中点如图,AB//CD,点 E 是 BC 的中点.可延长 DE 交 AB 于点 F. 模型 3:中位线如图,在△ABC 中,点 D 是 AB 边的中点.可作另一边 AC 的中点,构造三角形中位线.如下图所示:由中位线的性质可得,DE//BC 且 DE=1/2BC. 模型 4:连接直角顶点,构造斜中定理 【典例分析】【模型 1 倍长中线法】【典例 1】【阅读理解】课外兴趣小组活动时,老师提出了如下问题:如图 1,△ABC 中,若 AB=8,AC=6,求 BC 边上的中线 AD 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长 AD 到点 E,使 DE=AD,请根据小明的方法思考:(1)由已知和作图能得到△ADC≌△EDB 的理由是 .A.SSS B.SAS C.AAS D.HL(2)求得 AD 的取值范围是 .A.6<AD<8 B.6≤AD≤8 C.1<AD<7 D.1≤AD≤7【感悟】解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.【问题解决】(3)如图 2,AD 是△ABC 的中线,BE 交 AC 于 E,交 AD 于 F,且 AE=EF.求证:AC=BF.【变式 1-1】(1)在△ABC 中,AB=5,AC=3,求 BC 边上的中线 AD 的取值范围.(2)受到(1)启发,请你证明下面的问题:如图,在△ABC 中,D 是 BC 边上的中点,DE⊥DF,DE 交 AB 于点 E,DF 交 AC 于点 F,连接 EF.求证:BE+CF>EF.【变式 1-2】如图,在△ABC 中,已知:点 D 是 BC 中点,连接 AD 并延长到点 E,连接BE.(1)请你添加一个条件使△ACD≌△EBD,并给出证明.(2)若 AB=5,AC=3,求 BC 边上的中线 AD 的取值范围.【变式 1-3】阅读下面...