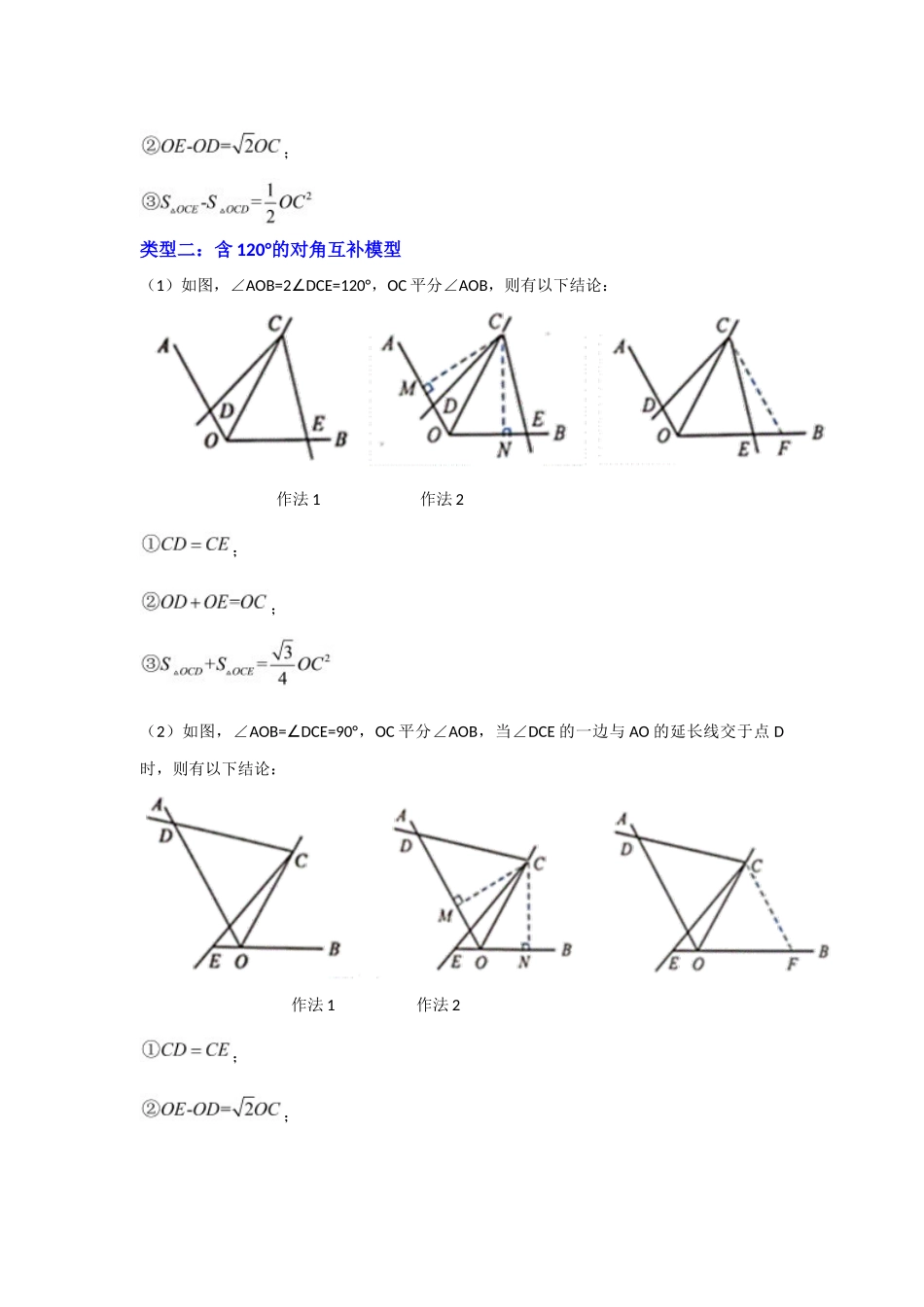
专题 05 对角互补模型综合应用(知识解读)【专题说明】共顶点模型,即四边形或构成的几何图形中,相对的角互补。主要:含 90°的对角互补,含120°的对角互补,两种类型,种类不同,得出的个别结论会有所区别。解决此类题型常用到的辅助线画法主要有两种:旋转法和过顶点作两垂线.【方法技巧】类型一:含 90°的对角互补模型(1)如图,∠AOB=DCE=90°∠,OC 平分∠AOB,则有以下结论: 作法 1 作法 2; ;(2)如图,∠AOB=DCE=90°∠,OC 平分∠AOB,当∠DCE 的一边与 AO 的延长线交于点 D时,则有以下结论: 作法 1 作法 2;;类型二:含 120°的对角互补模型(1)如图,∠AOB=2DCE=120°∠,OC 平分∠AOB,则有以下结论: 作法 1 作法 2;;(2)如图,∠AOB=DCE=90°∠,OC 平分∠AOB,当∠DCE 的一边与 AO 的延长线交于点 D时,则有以下结论: 作法 1 作法 2;;【典例分析】【类型一:含 90°的对角互补模型】【典例 1】(1)如图 1,在四边形 ABCD 中,AB=AD,∠B=∠D=90°,E、F 分别是边BC、CD 上的点,且∠EAF=∠BAD,线段 EF、BE、FD 之间的关系是 ;(不需要证明)(2)如图 2,在四边形 ABCD 中,AB=AD,∠B+∠D=180°,E、F 分别是边 BC、CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.(3)如图 3,在四边形 ABCD 中,AB=AD,∠B+∠D=180°,E、F 分别是边 BC、CD延长线上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.【变式 1-1】如图,在△ABC 中,AB=AC,∠BAC=90°,直角∠EPF 的顶点 P 是 BC 的中点,两边 PE、PF 分别交 AB、AC 于点 E、F,连接 EF 交 AP 于点 G,以下五个结论:①∠B=∠C=45°;② AP=EF;③∠AFP 和∠AEP 互补;④△EPF 是等腰直角三角形;⑤四边形 AEPF 的面积是△ABC 面积的,其中正确的结论是( )A.①②③B.①②④⑤C.①③④⑤D.①③④【变式 1-2】(1)如图 1,在四边形 ABCD 中,AB=AD,∠BAD=100°,∠B=∠ADC=90°.E,F 分别是 BC,CD 上的点.且∠EAF=50°.探究图中线段 EF,BE,FD 之间的数量关系.小 明 同 学 探 究 的 方 法 是 : 延 长 FD 到 点 G , 使 DG = BE , 连 接 AG , 先 证 明△AB...