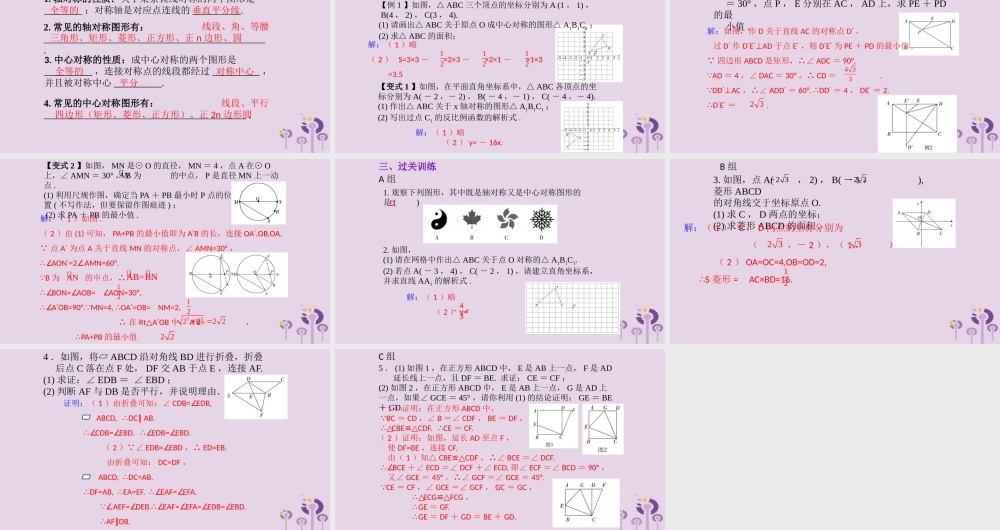
第七章 图形的变换与坐标第 31 课 轴对称与中心对称1. 轴对称的性质:关于某条直线对称的两个图形是________ ;对称轴是对应点连线的 __________.一、考点知识, 2. 常见的轴对称图形有: ______________________________________________.全等的3. 中心对称的性质:成中心对称的两个图形是__________ ,连接对称点的线段都经过 __________ ,并且被对称中心 __________.4. 常见的中心对称图形有:__________________________________________ .垂直平分线 线段、角、等腰三角形、矩形、菱形、正方形、正 n 边形、圆全等的对称中心平分 线段、平行四边形(矩形、菱形、正方形)、正 2n 边形圆【例 1 】如图,△ ABC 三个顶点的坐标分别为 A (1 , 1) , B(4 , 2) , C(3 , 4).(1) 请画出△ ABC 关于原点 O 成中心对称的图形△ A1B1C1 ;(2) 求△ ABC 的面积;【考点 1 】轴对称与中心对称的作图二、例题与变式解:( 1 )略( 2 ) S=3×3 - ×2×3 - ×2×1 - ×1×3 =3.5121212【变式 1 】如图,在平面直角坐标系中,△ ABC 各顶点的坐标分别为 A( - 2 ,- 2) , B( - 4 ,- 1) , C( - 4 ,- 4).(1) 作出△ ABC 关于 x 轴对称的图形△ A1B1C1 ;(2) 写出过点 C1 的反比例函数的解析式 .解:( 1 )略 ( 2 ) y= - 16x.【考点 2 】轴对称的性质【例 2 】如图,在矩形 ABCD 中, AD = 4 ,∠ DAC = 30° ,点 P , E 分别在 AC , AD 上,求 PE + PD的最 小值 .解:如图,作 D 关于直线 AC 的对称点 D′ , 过 D′ 作 D EAD′ ′⊥于点 E′ ,则 D E′ ′ 为 PE + PD 的最小值 . 四边形 ABCD 是矩形,∴∠ ADC = 90°. AD = 4 ,∠ DAC = 30° ,∴ CD = . DDAC′⊥,∴∠ ADD′ = 60°. DD∴′ = 4 , DE′ = 2.∴D E′ ′ = . 4 332 3解:( 1 )如图 .( 2 )由 (1) 可知, PA+PB 的最小值即为 A B′ 的长,连接 OA ,OB,OA,′ 点 A′ 为点 A 关于直线 MN 的对称点,∠ AMN=30° ,∴∠AON =2AMN=60°.′∠ B 为 的中点,∴ .∴∠BON= AOB= AON=30°,∠∠∴∠A OB=90°. MN=4, OA =OB= NM=2,′ ∴′ ∴ 在 Rt A OB△ ′中, A B= ′, ∴PA+PB 的最小值 .【变...