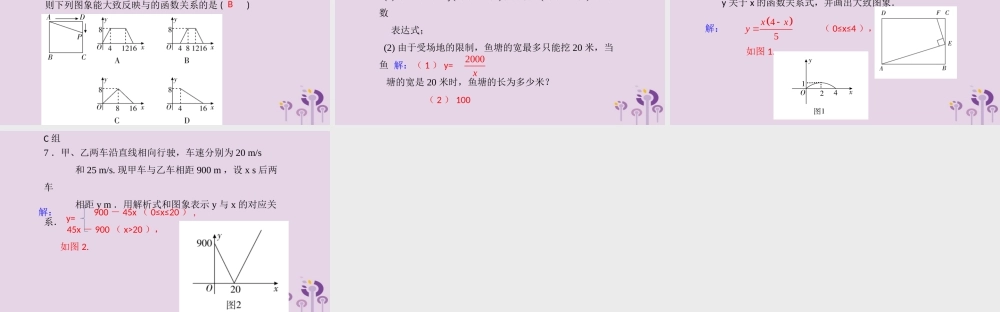
第三章 函数第 10 课 变量与函数1. 设在某变化过程中有两个变量 x , y ,对于在规定范围内的 x 的每一个值, y 都有唯一的值与之对应,那么就说 x 是自变量, y 是因变量,此时,也称 y 是 x 的函数 .一、考点知识B例:下列各曲线中,表示 y 是 x 的函数的是 ( )2.(1) 函数的三种表示法:解析法、列表法、 __________.(2) 由函数解析式画其图象的一般步骤: __________ 、 __________ 、 __________.(3) 函数自变量的取值范围:使函数解析式有 __________ 的自变量的取值的全体 .图象法列表描点连线意义【例 1 】求下列函数的自变量 x 的取值范围 .【考点 1 】函数自变量的取值范围二、例题与变式解:( 1 ) x≠1 (2) (3)1xyx 23yx1 2xyx(1) (2) (3)23x 12x 【变式 1 】求下列函数的自变量的取值范围 .解:( 1 ) ( 2 )全体实数 ( 3 ) x<2 且 x≠-2 231yx23yx2424xyx(1) (2) (3)13x 【考点 2 】函数的表示,实际问题中函数自变量 的取值范围【例 2 】一辆汽车油箱现有汽油 60 L ,如果不再加油, 那么 油箱中的油量 y( 单位: L) 随行驶里程 x( 单位: km) 的增加而 减少,平均耗油量为 0.1 L/km. (1) 写出 y 关于 x 的函数关系式; (2) 指出自变量 x 的取值范围; (3) 汽车行驶 200 km 时,油箱中还有多少汽油?解:( 1 ) y=60 - 0.1x ( 2 ) 0≤x≤600 ( 3 ) 40 【变式 2 】分别写出下列函数关系式,并指出其中自变 量的取值范围: (1) 一个等腰三角形的周长为 16 cm ,底边长 y( 单位: cm) 关于 腰长 x( 单位: cm) 的函数关系式; (2) 某运动员在 400m 一圈的跑道上训练,他跑一圈所用的时间 t ( 单位: s) 与速度 v( 单位: m/s) 的函数关系式; (3) 梯形的上底长 3 cm ,高 2 cm ,下底长 x cm 大于上底长但不超 过 5 cm. 写出梯形面积 S 关于 x 的函数解析式 .解:( 1 ) y=16 - 2x ( 00 ) ( 3 ) s=3+x ( 3