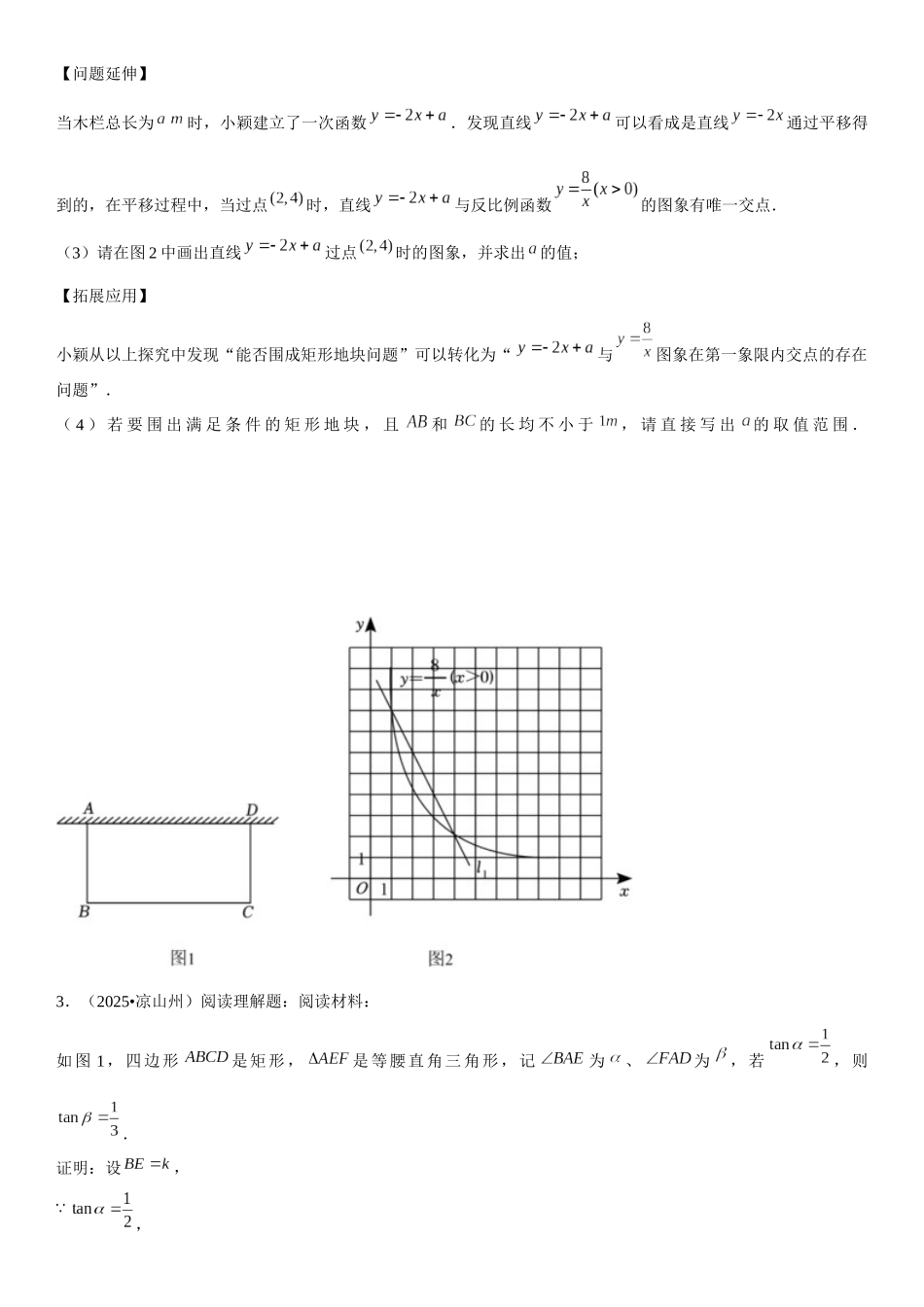
方法必备 04 新定义与阅读理解归纳迁移探究题(9 个考点 25 年中考真题大题 50 题专练) 一.反比例函数的应用(共 1 小题) 二.反比例函数综合题(共 2 小题)三.二次函数综合题(共 7 小题) 四.三角形综合题(共 5 小题)五.四边形综合题(共 18 小题 六.圆周角定理(共 1 小题)七.圆的综合题(共 4 小题) 八.几何变换综合题(共 4 小题)九.相似形综合题(共 8 小题)一.反比例函数的应用(共 1 小题)1.(2025•达州)【背景】在一次物理实验中,小冉同学用一固定电压为的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡(灯丝的阻值 亮度的实验(如图),已知串联电路中,电流与电阻、之间关系为,通过实验得出如下数据:1346432.42(1) , ;(2)【探究】根据以上实验,构建出函数,结合表格信息,探究函数的图象与性质.① 在平面直角坐标系中画出对应函数的图象;② 随着自变量的不断增大,函数值的变化趋势是 .(3)【拓展】结合(2)中函数图象分析,当时,的解集为 .二.反比例函数综合题(共 2 小题)2.(2025•济南)综合与实践如图 1,某兴趣小组计划开垦一个面积为的矩形地块种植农作物,地块一边靠墙,另外三边用木栏围住,木栏总长为.【问题提出】小组同学提出这样一个问题:若,能否围出矩形地块?【问题探究】小颖尝试从“函数图象”的角度解决这个问题:设为,为.由矩形地块面积为,得到,满足条件的可看成是反比例函数的图象在第一象限内点的坐标;木栏总长为,得到,满足条件的可看成一次函数的图象在第一象限内点的坐标,同时满足这两个条件的就可以看成两个函数图象交点的坐标.如图 2,反比例函数的图象与直线的交点坐标为和 ,因此,木栏总长为时,能围出矩形地块,分别为:,;或 , .(1)根据小颖的分析思路,完成上面的填空;【类比探究】(2)若,能否围出矩形地块?请仿照小颖的方法,在图 2 中画出一次函数图象并说明理由;【问题延伸】当木栏总长为时,小颖建立了一次函数.发现直线可以看成是直线通过平移得到的,在平移过程中,当过点时,直线与反比例函数的图象有唯一交点.(3)请在图 2 中画出直线过点时的图象,并求出的值;【拓展应用】小颖从以上探究中发现“能否围成矩形地块问题”可以转化为“与图象在第一象限内交点的存在问题”.( 4 ) 若 要 围 出 满 足 条 件 的 矩 形 地 块 , 且和的 长...