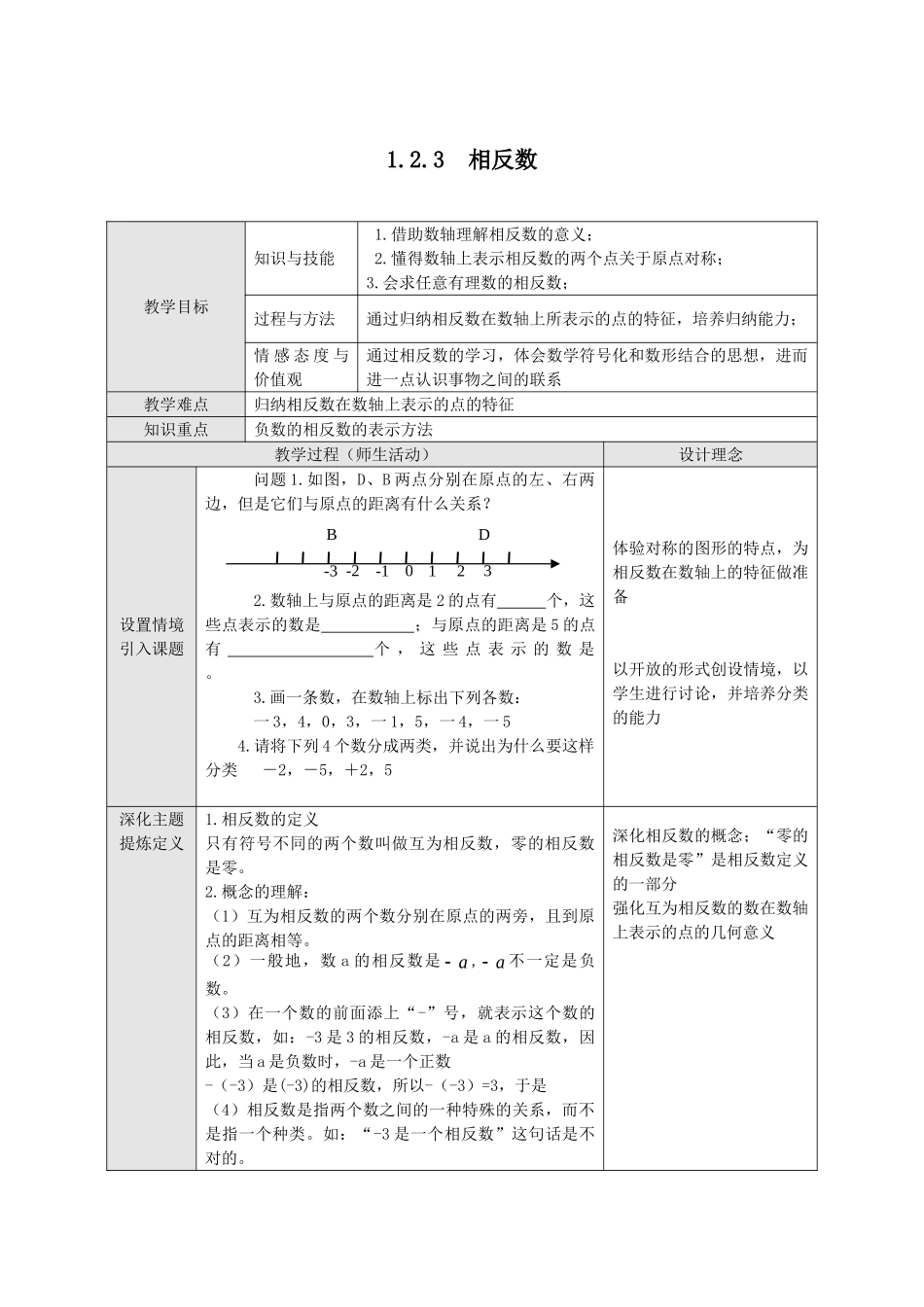
1.2.3 相反数教学目标知识与技能1.借助数轴理解相反数的意义;2.懂得数轴上表示相反数的两个点关于原点对称;3.会求任意有理数的相反数;过程与方法通过归纳相反数在数轴上所表示的点的特征,培养归纳能力;情 感 态 度 与价值观通过相反数的学习,体会数学符号化和数形结合的思想,进而进一点认识事物之间的联系教学难点归纳相反数在数轴上表示的点的特征知识重点负数的相反数的表示方法教学过程(师生活动)设计理念设置情境引入课题问题 1.如图,D、B 两点分别在原点的左、右两边,但是它们与原点的距离有什么关系?2.数轴上与原点的距离是 2 的点有 个,这些点表示的数是 ;与原点的距离是 5 的点有 个 , 这 些 点 表 示 的 数 是 。3.画一条数,在数轴上标出下列各数:一 3,4,0,3,一 1,5,一 4,一 54.请将下列 4 个数分成两类,并说出为什么要这样分类 -2,-5,+2,5体验对称的图形的特点,为相反数在数轴上的特征做准备以开放的形式创设情境,以学生进行讨论,并培养分类的能力深化主题提炼定义1.相反数的定义只有符号不同的两个数叫做互为相反数,零的相反数是零。2.概念的理解:(1)互为相反数的两个数分别在原点的两旁,且到原点的距离相等。(2)一般地,数 a 的相反数是a,a不一定是负数。(3)在一个数的前面添上“-”号,就表示这个数的相反数,如:-3 是 3 的相反数,-a 是 a 的相反数,因此,当 a 是负数时,-a 是一个正数-(-3)是(-3)的相反数,所以-(-3)=3,于是(4)相反数是指两个数之间的一种特殊的关系,而不是指一个种类。如:“-3 是一个相反数”这句话是不对的。深化相反数的概念;“零的相反数是零”是相反数定义的一部分强化互为相反数的数在数轴上表示的点的几何意义30-1-221-3DB规律:一般地,数 a 的相反数可以表示为-a思考:数轴上表示相反数的两个点和原点有什么关系?应用举例解决问题1. 两人一组,一人任说一个有理数,请同伴说出它的相反数2. 填空 (1)-5.8 是 的相反数, 的相反数是-(+3),a 的相反数是 ,a-b 的相反数是 ,0的相反数是 . (2)正数的相反数是 ,负数的相反数是 __ ___, 的相反数是它本身3.下列判断不正确的有 ( ) ① 互为相反数的两个数一定不相等;②互为相反数的数在数轴上的点一定在原点的两边;③所有的有理数都有相反数;④相反数是符号相反的两个点. A.1 个 B.2 个 C.3 个 D.4 ...