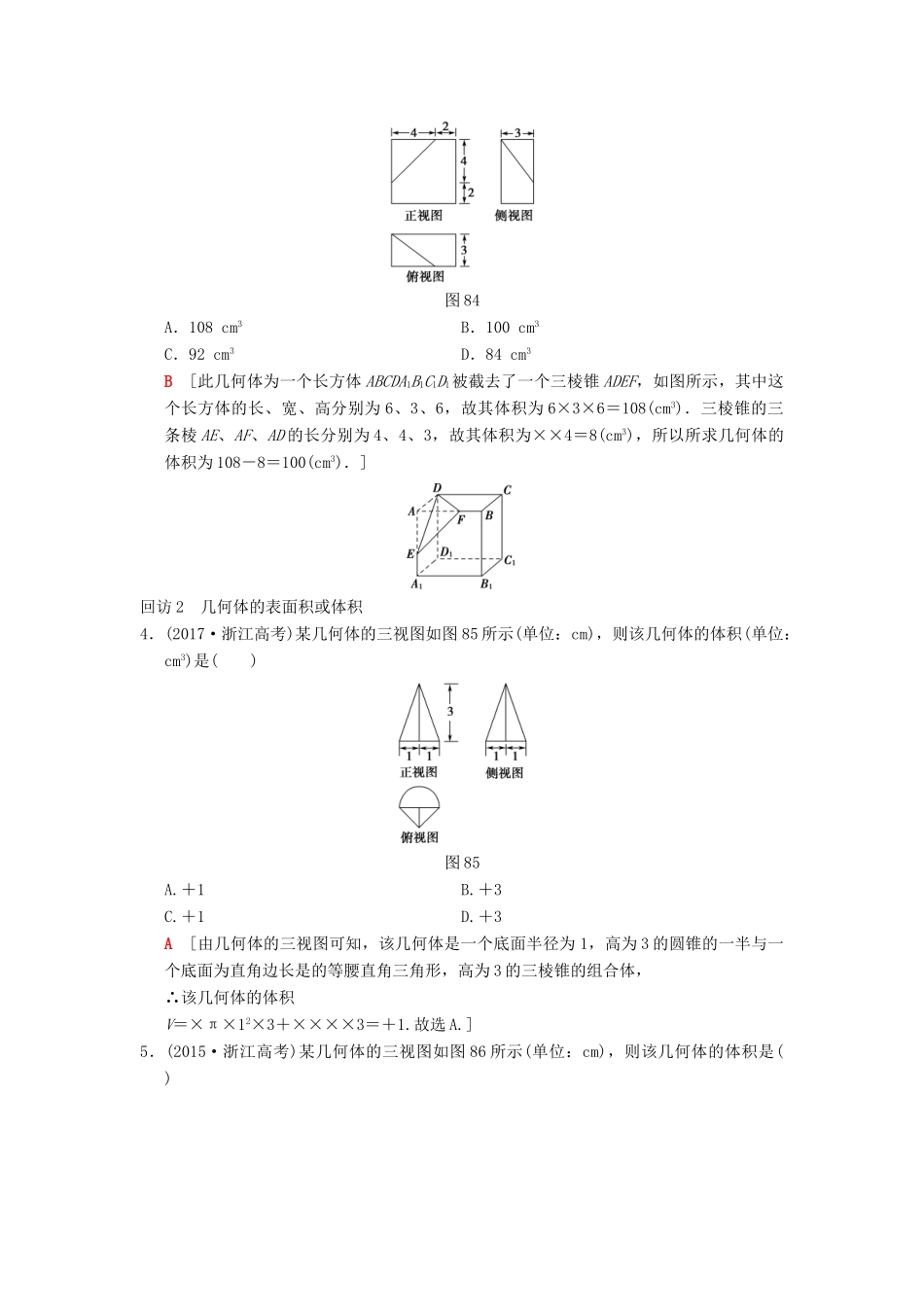
专题四 立体几何建知识网络 明内在联系[高考点拨] 立体几何专题是浙江新高考中当仁不让的热点之一,常以“两小一大”呈现 ,小题主要考查三视图与空间几何体的体积(特别是与球有关的体积)和空间位置关系及空间角,一大题常考空间位置关系的证明与空间角、距离的探求.本专题主要从“空间几何体表面积或体积的求解”“空间中的平行与垂直关系”“立体几何中的向量方法”三大角度进行典例剖析,引领考生明确考情并提升解题技能.突破点 8 空间几何体表面积或体积的求解 (对应学生用书第 29 页)[核心知识提炼]提炼 1 求解几何体的表面积或体积 (1)对于规则几何体,可直接利用公式计算.(2)对于不规则几何体,可采用割补法求解;对于某些三棱锥,有时可采用等体积转换法求解.(3)求解旋转体的表面积和体积时,注意圆柱的轴截面是矩形,圆锥的轴截面是等腰三角形,圆台的轴截面是等腰梯形的应用. 提炼 2 球与几何体的外接与内切 (1)正四面体与球:设正四面体的棱长为 a ,由正四面体本身的对称性,可知其内切球和外接球的球心相同,则内切球的半径 r = a ,外接球的半径 R = a .(2)正方体与球:设正方体 ABCDA1B1C1D1的棱长为 a,O 为其对称中心,E,F,H,G 分别为 AD,BC,B1C1,A1D1的中点,J 为 HF 的中点,如图 81 所示.图 81① 正方体的内切球:截面图为正方形 EFHG 的内切圆,故其内切球的半径为 OJ = ;② 正方体的棱切球:截面图为正方形 EFHG 的外接圆,故其棱切球的半径为 OG=;③ 正方体的外接球:截面图为矩形 ACC1A1的外接圆,故其外接球的半径为 OA 1=.[高考真题回访]回访 1 空间几何体的结构及三视图1.(2015·浙江高考)如图 82,斜线段 AB 与平面 α 所成的角为 60°,B 为斜足,平面 α上的动点 P 满足∠PAB=30°,则点 P 的轨迹是( )图 82A.直线B.抛物线C.椭圆D.双曲线的一支C [因为∠PAB=30°,所以点 P 的轨迹为以 AB 为轴线,PA 为母线的圆锥面与平面 α的交线,且平面 α 与圆锥的轴线斜交,故点 P 的轨迹为椭圆.]2.(2014·浙江高考)某几何体的三视图(单位:cm)如图 83 所示,则该几何体的体积是( )图 83A.72 cm3 B.90 cm3C.108 cm3D.138 cm3B [该几何体为一个组合体,左侧为三棱柱,右侧为长方体,如图所示.V=V 三棱柱+V长方体=×4×3×3+4×3×6=18+72=90(cm3).]3.(2013·浙江高考)已知某几何体的三视...