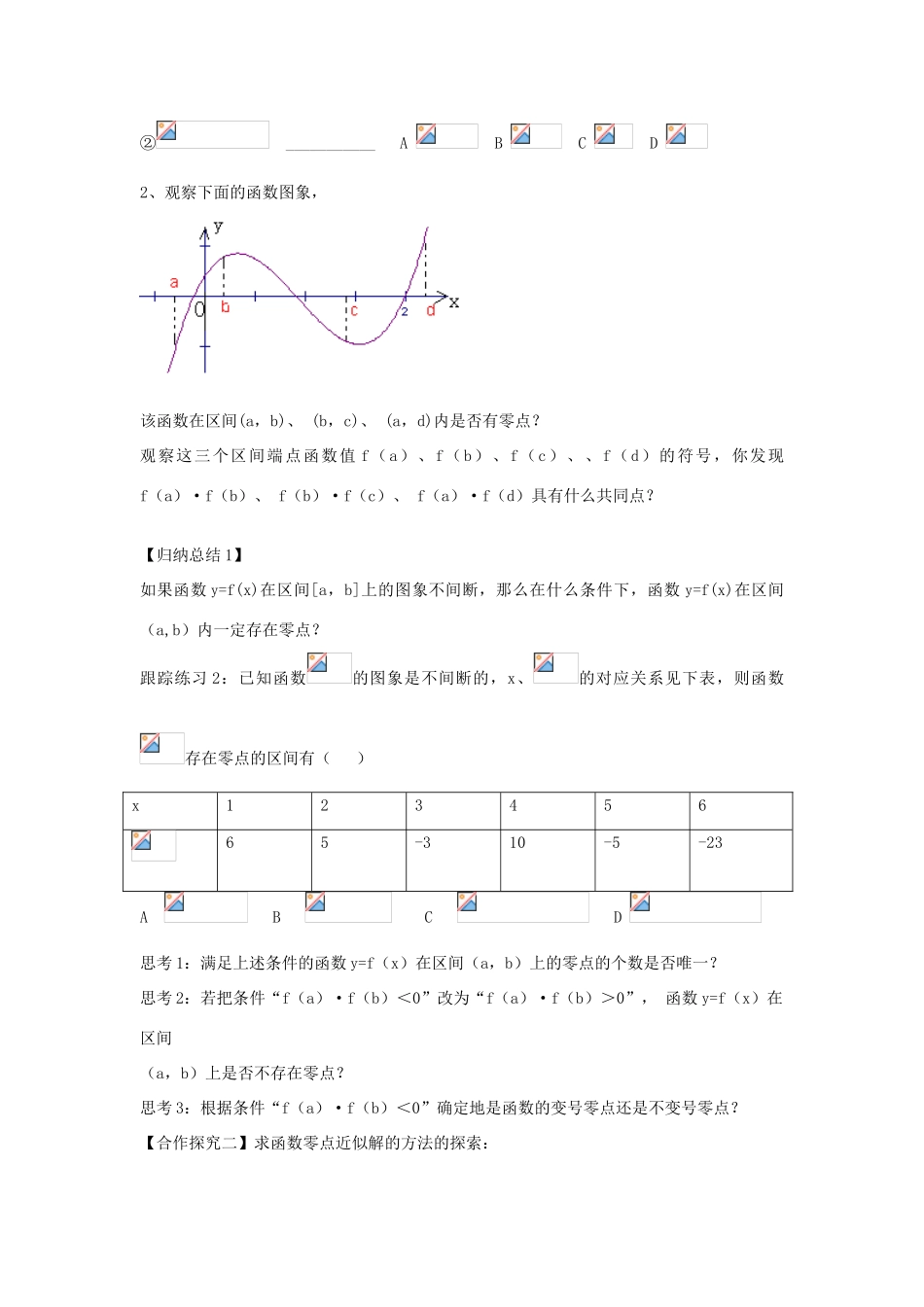
2.4.2《求函数零点近似解的一种计算方法——二分法》学案【学习目标】① 知识目标:掌握二分法求函数零点的一般方法,能借助计算器求函数近似零点。② 能力目标:了解“逼近”这一数学思想,感受体验二分法中的算法思想。③ 情感目标:通过合作学习,培养同学们的团结协作的思想品质。【自主学习】1、画出函数的图象,并找出它们的零点。观察上述图象,你发现它们在零点两侧函数值的符号有何不同?2、请给出变号零点与不变号零点的严格定义:如果函数图象 ,则称这样的零点为变号零点。如果函数图象 ,则称这样的零点为不变号零点。跟踪练习 1:函数 f(x)的图象如图所示,则该函数变号零点的个数是 个。【合作探究一】零点存在性的探索:1、请找出下列函数的零点所在的区间:① ___________ A B C D ② ___________ A B C D 2、观察下面的函数图象,该函数在区间(a,b)、 (b,c)、 (a,d)内是否有零点?观察这三个区间端点函数值 f(a)、f(b)、f(c)、、f(d)的符号,你发现 f(a)·f(b)、 f(b)·f(c)、 f(a)·f(d)具有什么共同点?【归纳总结 1】如果函数 y=f(x)在区间[a,b]上的图象不间断,那么在什么条件下,函数 y=f(x)在区间(a,b)内一定存在零点? 跟踪练习 2:已知函数的图象是不间断的,x、的对应关系见下表,则函数存在零点的区间有( )x12345665-310-5-23A B C D 思考 1:满足上述条件的函数 y=f(x)在区间(a,b)上的零点的个数是否唯一?思考 2:若把条件“f(a)·f(b)<0”改为“f(a)·f(b)>0”, 函数 y=f(x)在区间(a,b)上是否不存在零点?思考 3:根据条件“f(a)·f(b)<0”确定地是函数的变号零点还是不变号零点?【合作探究二】求函数零点近似解的方法的探索:1、函数在下列哪个区间内有零点 ( )A B C D 2、不用求根公式,如何求函数 f(x)=x2-2x-1 在区间(2,3)上的零点近似值(精确到0.1)?解:由于 f(2)=-1<0,f(3)=3>0,可以确定区间[2,3]作为计算的初始区间。端点或中点横坐标计算端点或中点的函数值定区间a0=2,b0=3f(2)=-1<0,f(3)=3>0[2,3]因 为 , 所 以 。【归纳总结 2】回顾上述求解过程,思考以下问题:⑴ 求函数 f(x)的零点近似解第一步应做什么? ⑵ 如何缩小零点所在的区间(a,b)? 若 f(c)=0 说明什么? 若 f(a)·f(c)<0 又说明什么? ⑶ 若给定精确度,如何选取零点近似值?...