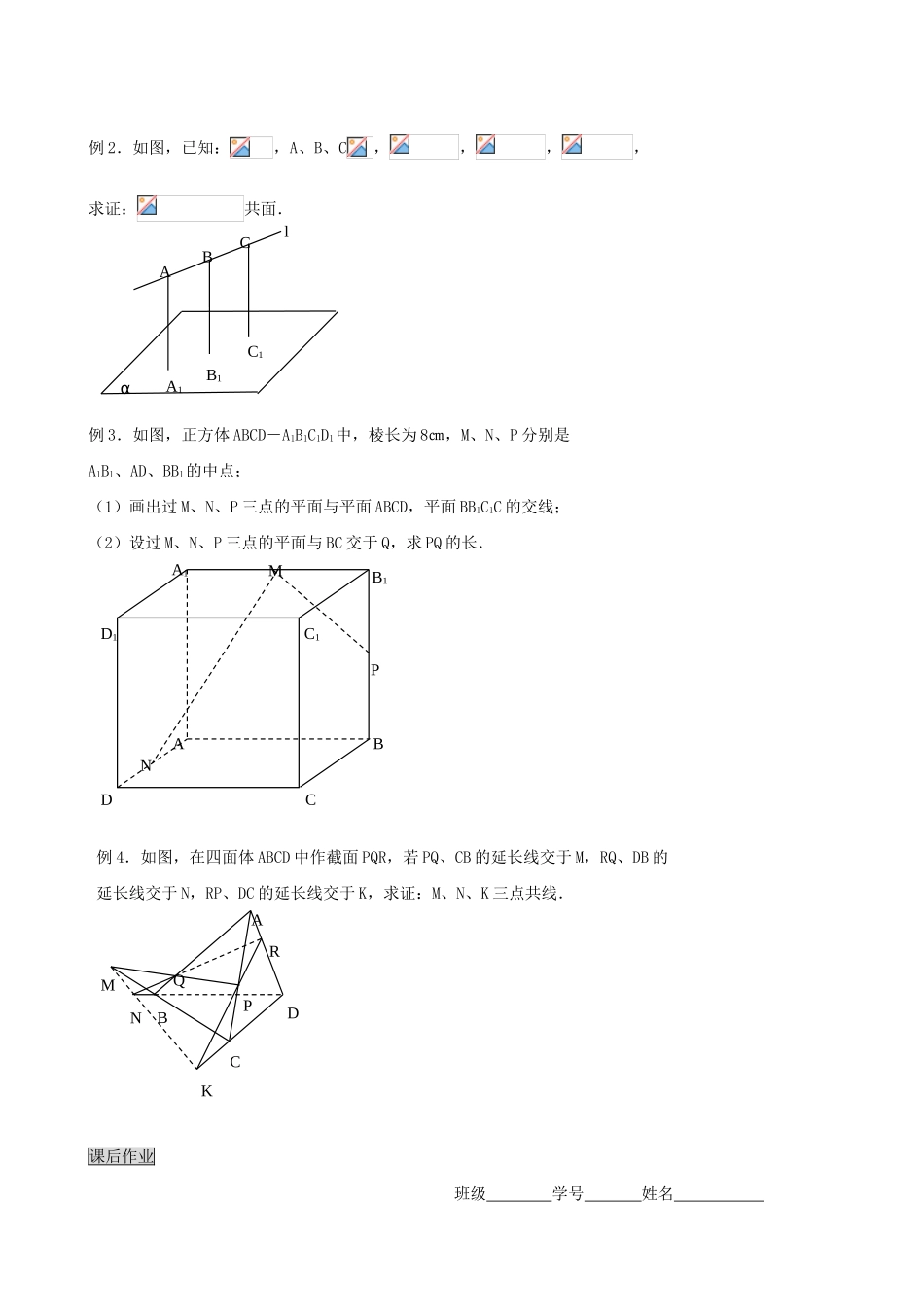
高三数学教学案 第九章 直线、平面、简单几何体 第一课时 平面的基本性质考纲摘录掌握平面的基本性质;会用斜二侧画法画水平放置的平面图形的直观图,理解用反证法证明命题的思路,会用反证法证明一些简单的问题.知识概要 (1)平面的基本性质(三个公理及其三个推论)及其运用(证明三线共点,三点共线,三线共面);(2)水平放置的平面图形的直观图的画法——斜二测画法的规则;(3)会用间接证法证明命题(反证法,同一法).重点难点(1)运用公理证明三线共点、三点共线;(2)掌握“图形语言”、“符号语言” .基础练习1.下列命题中,正确的是( )A.首尾相接的四条线段在同一平面内;B.三条互相平行的线段在同一平面内;C.两两相交的三条直线在同一平面内;D.若四个点中的三个点在同一直线上,那么这四个点在同一平面内.2.下列四个推理过程,错误的是( )A. ∥,;B.C.D.A、B、C,A、B、C且 A、B、C 不共线与重合3.一个水平放置的平面图形的斜二侧直观图是一个底角为 45°,腰和上底长均为 1 的等腰梯形,则这个平面图形的面积是( )A.B.C.D.4.不重合的三条直线,若相交于一点,可以确定____________平面;若相交于两点可确定__________平面;若相交于三点可确定_________平面.例题讲解例 1.如图,已知在空间四边形 ABCD 中,E、F 分别是 AB、AD 的中点,G、H 分别是 BC、CD 上的点,且,求证:直线 EG、FH、AC 相交于一点.CADFEBGH例 2.如图,已知:,A、B、C,,,,求证:共面.例 3.如图,正方体 ABCD-A1B1C1D1中,棱长为 8㎝,M、N、P 分别是A1B1、AD、BB1的中点;(1)画出过 M、N、P 三点的平面与平面 ABCD,平面 BB1C1C 的交线;(2)设过 M、N、P 三点的平面与 BC 交于 Q,求 PQ 的长.例 4.如图,在四面体 ABCD 中作截面 PQR,若 PQ、CB 的延长线交于 M,RQ、DB 的延长线交于 N,RP、DC 的延长线交于 K,求证:M、N、K 三点共线.课后作业 班级 学号 姓名 CD1DNMC1B1A1ABPlABCA1B1C1αBPKNCADMQR1.下列命题中不正确的是( )① 一条直线和两条平行直线都相交,那么这三条直线共面;② 每两条都相交,但不共点的四条直线一定共面;③ 两条互相垂直的直线共面;④ 两条直线都和第三条相交,那么这两条直线可以确定一个平面A.①与②B.③与④C.①与③D.②与④2.一条直线和它外面不共线的三点可以确定的平面的个数( )A.1 个...