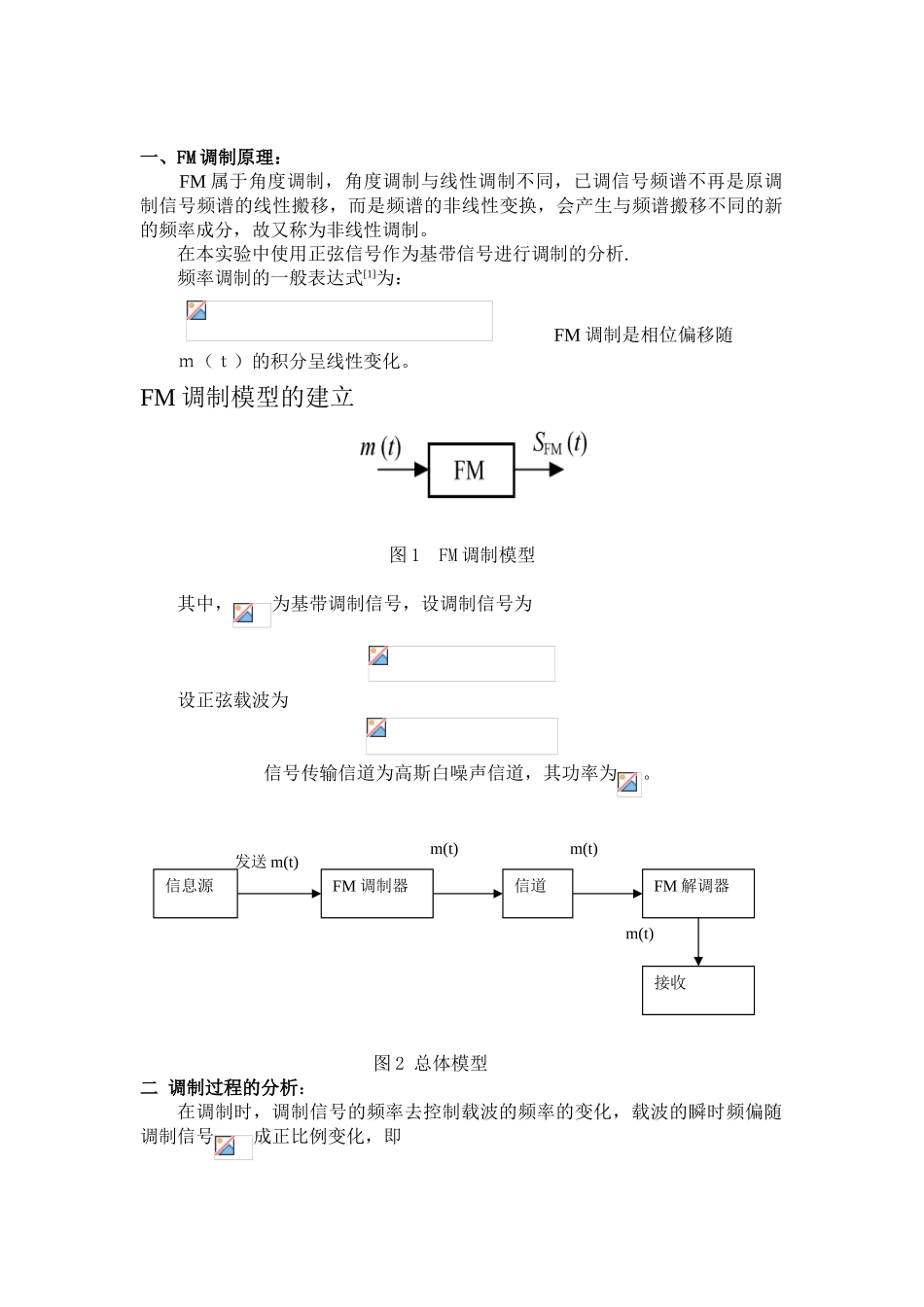
一、FM 调制原理: FM 属于角度调制,角度调制与线性调制不同,已调信号频谱不再是原调制信号频谱的线性搬移,而是频谱的非线性变换,会产生与频谱搬移不同的新的频率成分,故又称为非线性调制。在本实验中使用正弦信号作为基带信号进行调制的分析. 频率调制的一般表达式[1]为: FM 调制是相位偏移随m(t)的积分呈线性变化。FM 调制模型的建立图 1 FM 调制模型其中,为基带调制信号,设调制信号为设正弦载波为信号传输信道为高斯白噪声信道,其功率为。图 2 总体模型二 调制过程的分析:在调制时,调制信号的频率去控制载波的频率的变化,载波的瞬时频偏随调制信号成正比例变化,即发送 m(t)信息源m(t)m(t)m(t)FM 调制器信道FM 解调器接收式中,为调频灵敏度()。这时相位偏移为则可得到调频信号为FM 调制 1. 对 FM 调制信号的频谱分析 clear allts=0.00125; %信号抽样时间间隔t=0:ts:10-ts; %时间向量am=10;fs=1/ts; %抽样频率df=fs/length(t); %fft的频率分辨率msg=am*cos(2*pi*10*[0:0.01:0.99]); msg1=msg'*ones(1,fs/10); %扩展成取样信号形式msg2=reshape(msg1.',1,length(t));Pm=fft(msg2); %求消息信号的频谱f=-fs/2:df:fs/2-df; subplot(3,1,1)plot(t,fft(abs(Pm)))title('消息信号频谱')m=fft(msg,1024); %对msg进行傅利叶变换N=(0:length(m)-1)*fs/length(m)-fs/2;subplot(3,1,2)plot(N,abs(m)); %调制信号频谱图title('调制信号频谱')int_msg(1)=0; %消息信号积分for ii=1:length(t)-1 int_msg(ii+1)=int_msg(ii)+msg2(ii)*ts;endkf=50;fc=250; %载波频率Sfm=am*cos(2*pi*fc*t+2*pi*kf*int_msg); %调频信号Pfm=fft(Sfm)/fs; % FM信号频谱subplot(3,1,3);plot(f,fftshift(abs(Pfm))) % 画出已调信号频谱title('FM信号频谱')Pc=sum(abs(Sfm).^2)/length(Sfm) %已调信号功率Ps=sum(abs(msg2).^2)/length(msg2) %消息信号功率fm=50;betaf=kf*max(msg)/fm % 调制指数W=2*(betaf+1)*fm % 调制信号带宽用FFT函数进行傅利叶变换,进行傅立叶变化便分别得到调制信号与调制之后的FM信号的频谱图如下:012345678910-202x 105消 息 信 号 频 谱-500-400-300-200-10001002003004005000200400600调 制 信 号 频 谱-500-400-300-200-10001002003004005000510FM信 号 频 谱 图2-5通过频谱图的对比比较我们可以看出FM调制并不是使原正弦信号的频谱在原来位置上通过移动得到调制波形...