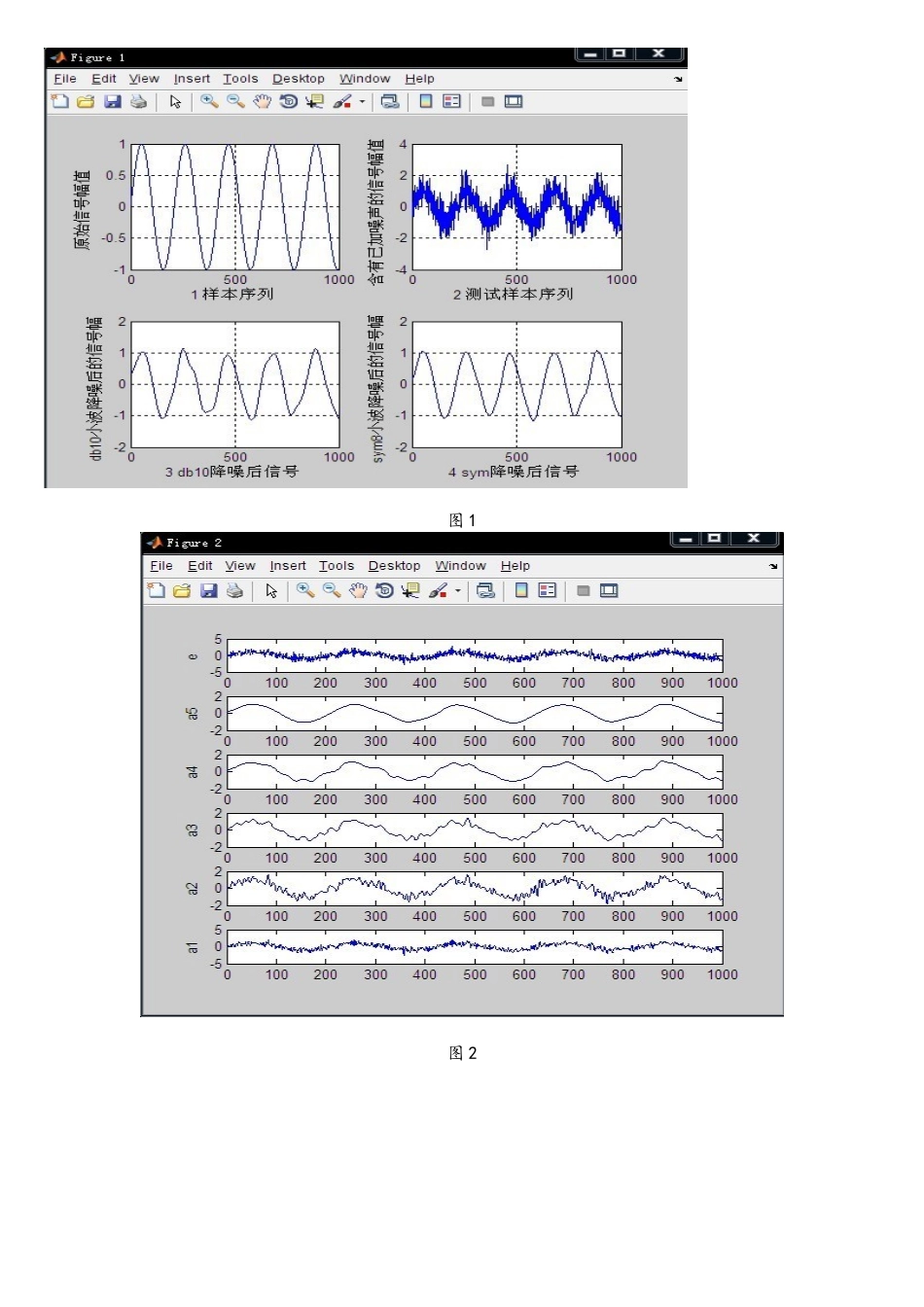
基于小波变换的信号降噪讨论2 小波分析基本理论设 Ψ(t)∈L 2( R) ( L 2( R) 表示平方可积的实数空间,即能量有限的信号空间) , 其傅立叶变换为 Ψ(t).当 Ψ(t)满足条件[4,7]: (1) 时,我们称 Ψ(t)为一个基本小波或母小波,将母小波函数 Ψ(t)经伸缩和平移后,就可以得到一个小波序列: (2)其中 a 为伸缩因子,b 为平移因子。对于任意的函数 f(t)∈L 2( R)的连续小波变换为:(3)其逆变换为: (4)小波变换的时频窗是可以由伸缩因子 a 和平移因子 b 来调节的,平移因子 b,可以改变窗口在相平面时间轴上的位置,而伸缩因子 b 的大小不仅能影响窗口在频率轴上的位置,还能改变窗口的形状。小波变换对不同的频率在时域上的取样步长是可调节的,在低频时,小波变换的时间分辨率较低,频率分辨率较高:在高频时,小波变换的时间分辨率较高,而频率分辨率较低.使用小波变换处理信号时,首先选取适当的小波函数对信号进行分解,其次对分解出的参数进行阈值处理,选取合适的阈值进行分析,最后利用处理后的参数进行逆小波变换,对信号进行重构。3 小波降噪的原理和方法3。1 小波降噪原理从信号学的角度看 ,小波去噪是一个信号滤波的问题。尽管在很大程度上小波去噪可以看成是低通滤波 ,但由于在去噪后 ,还能成功地保留信号特征 ,所以在这一点上又优于传统的低通滤波器。由此可见 ,小波去噪实际上是特征提取和低通滤波的综合 ,其流程框图如图所示[6]:小波分析的重要应用之一就是用于信号消噪 ,一个含噪的一维信号模型可表示为如下形式: k=0.1…….n—1其中 ,f( k)为有用信号,s(k)为含噪声信号,e(k)为噪声,ε 为噪声系数的标准偏差。假设 e(k)为高斯白噪声,通常情况下有用信号表现为低频部分或是一些比较平稳的信号,而噪声信号则表现为高频的信号,下面对 s(k)信号进行如图结构的小波分解,则噪声部分通常包含在 Cd1、Cd2、Cd3 中,只要对 Cd1,Cd2,Cd3 作相应的小波系数处理,然后对信号进行重构即可以达到消噪的目的。特征提取低通滤波特征信号重建信号带噪信号3.2 降噪方法一般来说, 一维信号的降噪过程可以分为 3 个步骤进行[5,6]:1)一维信号的小波分解,选择一个小波并确定一个小波分解的层次 N,然后对信号进行 N 层小波分解计算。2)小波分解高频系数的阈值量化,对第 1 层到第 N 层的每一层高频系数, 选择一个阈值进行软阈值量化处理. 3)一维小波...