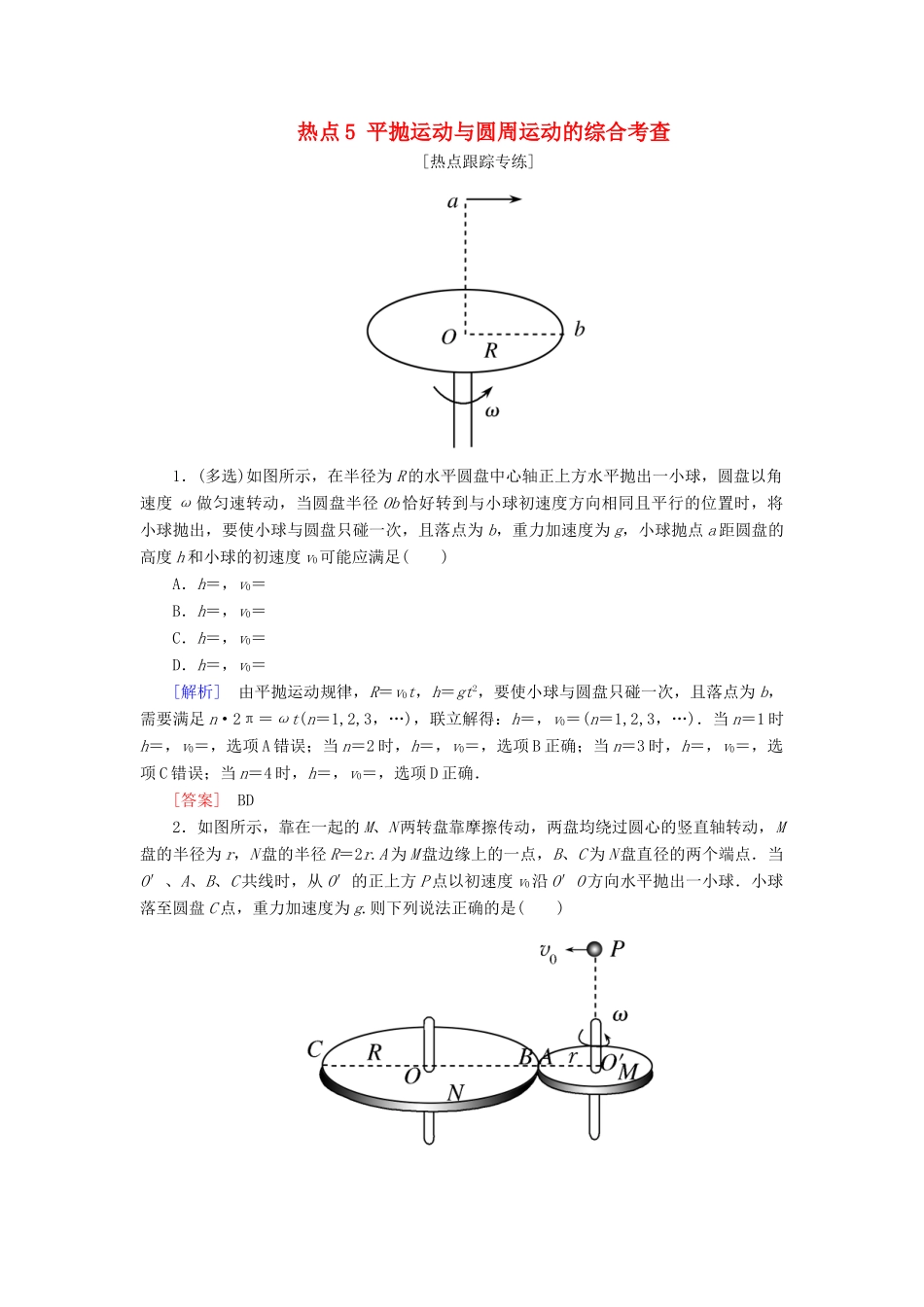
热点 5 平抛运动与圆周运动的综合考查[热点跟踪专练]1.(多选)如图所示,在半径为 R 的水平圆盘中心轴正上方水平抛出一小球,圆盘以角速度 ω 做匀速转动,当圆盘半径 Ob 恰好转到与小球初速度方向相同且平行的位置时,将小球抛出,要使小球与圆盘只碰一次,且落点为 b,重力加速度为 g,小球抛点 a 距圆盘的高度 h 和小球的初速度 v0可能应满足( )A.h=,v0=B.h=,v0=C.h=,v0=D.h=,v0=[解析] 由平抛运动规律,R=v0t,h=gt2,要使小球与圆盘只碰一次,且落点为 b,需要满足 n·2π=ωt(n=1,2,3,…),联立解得:h=,v0=(n=1,2,3,…).当 n=1 时h=,v0=,选项 A 错误;当 n=2 时,h=,v0=,选项 B 正确;当 n=3 时,h=,v0=,选项 C 错误;当 n=4 时,h=,v0=,选项 D 正确.[答案] BD2.如图所示,靠在一起的 M、N 两转盘靠摩擦传动,两盘均绕过圆心的竖直轴转动,M盘的半径为 r,N 盘的半径 R=2r.A 为 M 盘边缘上的一点,B、C 为 N 盘直径的两个端点.当O′、A、B、C 共线时,从 O′的正上方 P 点以初速度 v0沿 O′O 方向水平抛出一小球.小球落至圆盘 C 点,重力加速度为 g.则下列说法正确的是( )A.若 M 盘转动角速度 ω=,则小球抛出时到 O′的高度为B.若小球抛出时到 O′的高度为,则 M 盘转动的角速度必为 ω=C.只要 M 盘转动角速度满足 ω=(n∈N*),小球就可能落至 C 点D.只要小球抛出时到 O′的高度恰当,小球就可能落至 C 点[解析] 小球能落在 C 点,运动时间有两种可能:当 C 点离 O′最近时,r=v0t1;当 C点离 O′最远时,5r=v0t2.在这两种情况下,小球抛出时离 O′的高度应满足 h1=gt=或 h2=gt=.由于两盘边缘线速度大小相等,ωMr=ωNR,因此 M 盘的角速度是 N 盘的两倍,对应的角速度应满足 ω1==(n∈N)和 ω2==(n∈N*),当 n=0 时,A 选项正确;B 选项只给出了 n=0 的情况,因此 B 项错误;对比 ω2可知 C 选项错误;在满足小球抛出时离 O′的高度的情况下,还应满足 M 盘转动的角速度关系,才能保证小球落在 C 点,D 项错误.[答案] A3.(多选)如图所示,半径为 R 的圆弧轨道与半径为的光滑半圆弧轨道通过图示方式组合在一起,A、B 分别为半圆弧轨道的最高点和最低点,O 为半圆弧的圆心.现让一可视为质点的小球从 B 点以一定的初速度沿半圆弧轨道运动...