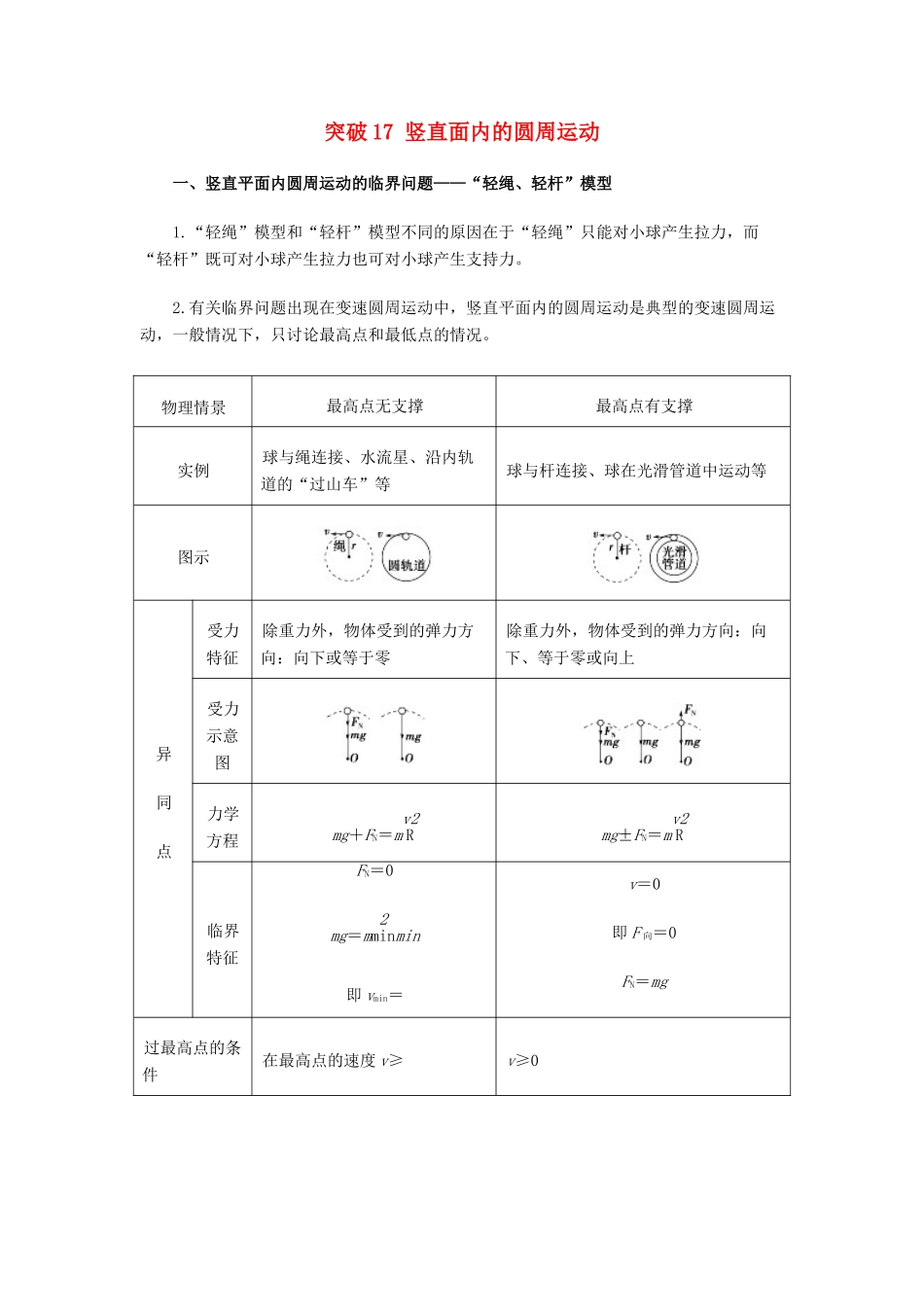
突破 17 竖直面内的圆周运动一、竖直平面内圆周运动的临界问题——“轻绳、轻杆”模型1.“轻绳”模型和“轻杆”模型不同的原因在于“轻绳”只能对小球产生拉力,而“轻杆”既可对小球产生拉力也可对小球产生支持力。2.有关临界问题出现在变速圆周运动中,竖直平面内的圆周运动是典型的变速圆周运动,一般情况下,只讨论最高点和最低点的情况。物理情景最高点无支撑最高点有支撑实例球与绳连接、水流星、沿内轨道的“过山车”等球与杆连接、球在光滑管道中运动等图示异同点受力特征除重力外,物体受到的弹力方向:向下或等于零除重力外,物体受到的弹力方向:向下、等于零或向上受力示意图力学方程mg+FN=mv2Rmg±FN=mv2R临界特征FN=0mg=m2minmin即 vmin=v=0即 F 向=0FN=mg过最高点的条件 在最高点的速度 v≥v≥0 【典例 1】如图甲所示,轻杆一端固定在 O 点,另一端固定一小球,现让小球在竖直平面内做半径为 R 的圆周运动。小球运动到最高点时,杆与小球间弹力大小为 F,小球在最高点的速度大小为 v,其 F-v2图象如图乙所示,则( ) A.小球的质量为aRbB.当地的重力加速度大小为RbC.v2=c 时,小球对杆的弹力方向向上D.v2=2b 时,小球受到的弹力与重力大小相等【答案】: ACD 【典例 2】用长 L = 0.6 m 的绳系着装有 m = 0.5 kg 水的小桶,在竖直平面内做圆周运动,成为“水流星”。G =10 m/s2。求: (1) 最高点水不流出的最小速度为多少?(2) 若过最高点时速度为 3 m/s,此时水对桶底的压力多大?【答案】 (1) 2.45 m/s (2) 2.5 N 方向竖直向上【解析】(1) 水做圆周运动,在最高点水不流出的条件是:水的重力不大于水所需要的向心力。这是最小速度即是过最高点的临界速度 v0。以水为研究对象, mg=m0解得 v0== m/s ≈ 2.45 m/s(2) 因为 v = 3 m/s>v0,故重力不足以提供向心力,要由桶底对水向下的压力补充,此时所需向心力由以上两力的合力提供。V = 3 m/s>v0,水不会流出。设桶底对水的压力为 F,则由牛顿第二定律有:mg+F=mv2L解得 F=mv2L -mg=0.5×(320.6-10)N=2.5N根据牛顿第三定律 F′=-F所以水对桶底的压力 F′=2.5N,方向竖直向上。【跟踪短训】1. 如图所示,一内壁光滑、质量为 m、半径为 r 的环形细圆管,用硬杆竖直固定在天花板上.有一质量为 m 的小球(可看做质点)在圆管中运动.小球以速率 v0经过圆管最低点时,杆对圆管...