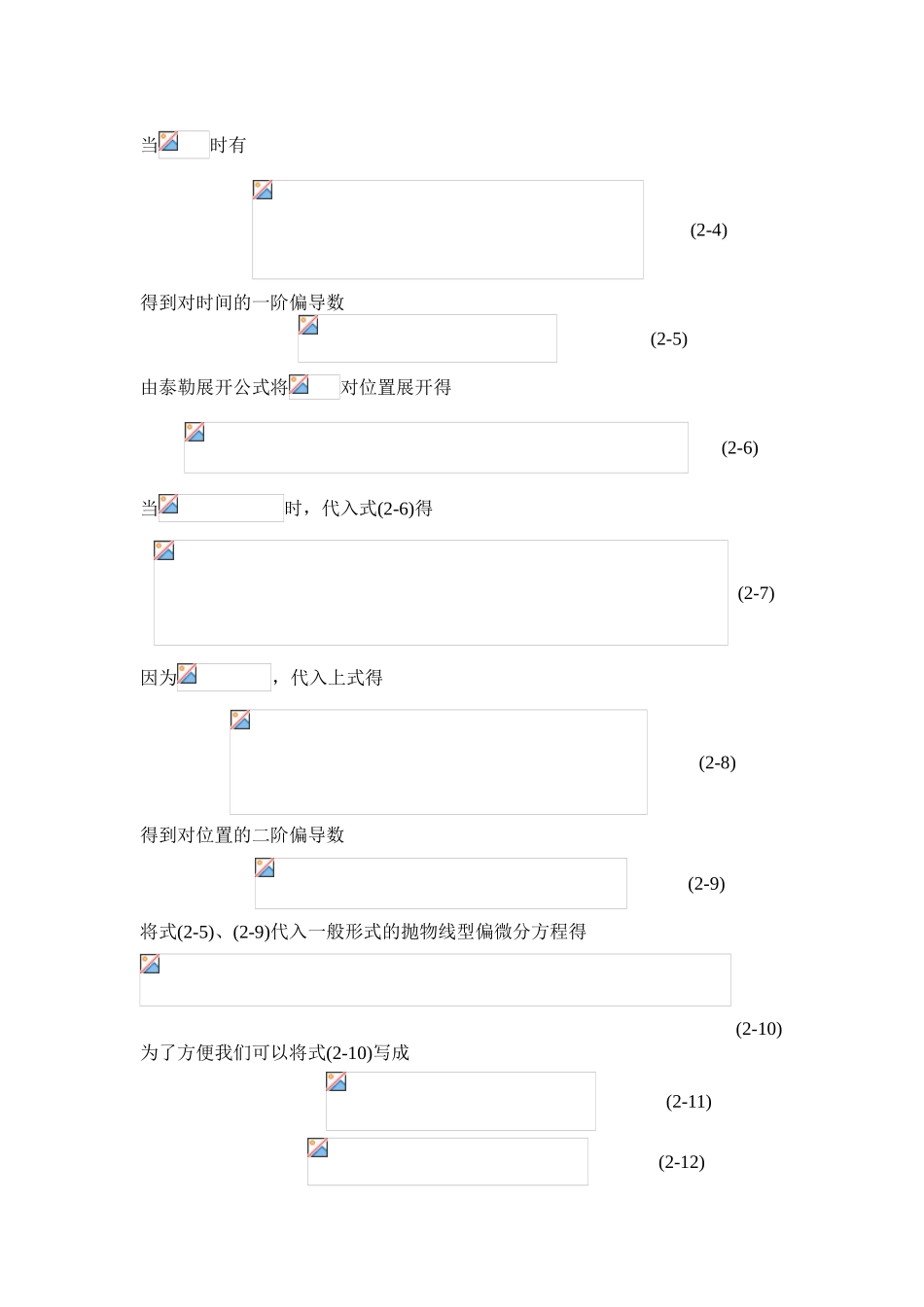
任课老师评语: 签名: 年 月 日南京理工大学课程考核论文课程名称: 高等数值分析 论文题目: 有限差分法求解偏微分方程 姓 名: 罗 晨 学 号: 115104000545 成 绩: 有限差分法求解偏微分方程一、主要内容1.有限差分法求解偏微分方程,偏微分方程如一般形式的一维抛物线型方程:具体求解的偏微分方程如下:2.推导五种差分格式、截断误差并分析其稳定性;3.编写 MATLAB 程序实现五种差分格式对偏微分方程的求解及误差分析;4.结论及完成本次实验报告的感想。二、推导几种差分格式的过程:有限差分法(finite-difference methods)是一种数值方法通过有限个微分方程近似求导从而寻求微分方程的近似解。有限差分法的基本思想是把连续的定解区域用有限个离散点构成的网格来代替;把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似;把原方程和定解条件中的微商用差商来近似,积分用积分和来近似,于是原微分方程和定解条件就近似地代之以代数方程组,即有限差分方程组,解此方程组就可以得到原问题在离散点上的近似解。推导差分方程的过程中需要用到的泰勒展开公式如下: (2-1)求解区域的网格划分步长参数如下: (2-2)2.1 古典显格式2.1.1 古典显格式的推导由泰勒展开公式将对时间展开得 (2-3)当时有 (2-4)得到对时间的一阶偏导数 (2-5)由泰勒展开公式将对位置展开得 (2-6)当时,代入式(2-6)得 (2-7)因为,代入上式得 (2-8)得到对位置的二阶偏导数 (2-9)将式(2-5)、(2-9)代入一般形式的抛物线型偏微分方程得(2-10)为了方便我们可以将式(2-10)写成 (2-11) (2-12)最后得到古典显格式的差分格式为 (2-13),古典显格式的差分格式的截断误差是。2.1.2 古典显格式稳定性分析古典显格式(2-13)写成矩阵形式为 (2-14)上面的 C 矩阵的特征值是: (2-15)使,即结论:当时,所以古典显格式是稳定的。2.2 古典隐格式2.2.1 古典隐格式的推导将代入式 (2-3)得 (2-16) (2-17)得到对时间的一阶偏导数 (2-18)将式(2-9)、(2-18)原方程得到(2-19)为了方便把(2-19)写成 (2-20) (2-21)最后得到古典隐格式的差分格式为 (2-22),古典隐格式的差分格式的截断误差是。2.2.2 古典隐格式稳定性分析将古典隐格式(2-22)写成矩阵形式如下 (2-23)误差传播方程 (2-24)所以误差方程的系数矩阵为使,显然 恒成立。结论:对于,即任意网格比下,古典隐格式是绝对稳定的。2.3 Richardson 格式2.3.1 Richardson...