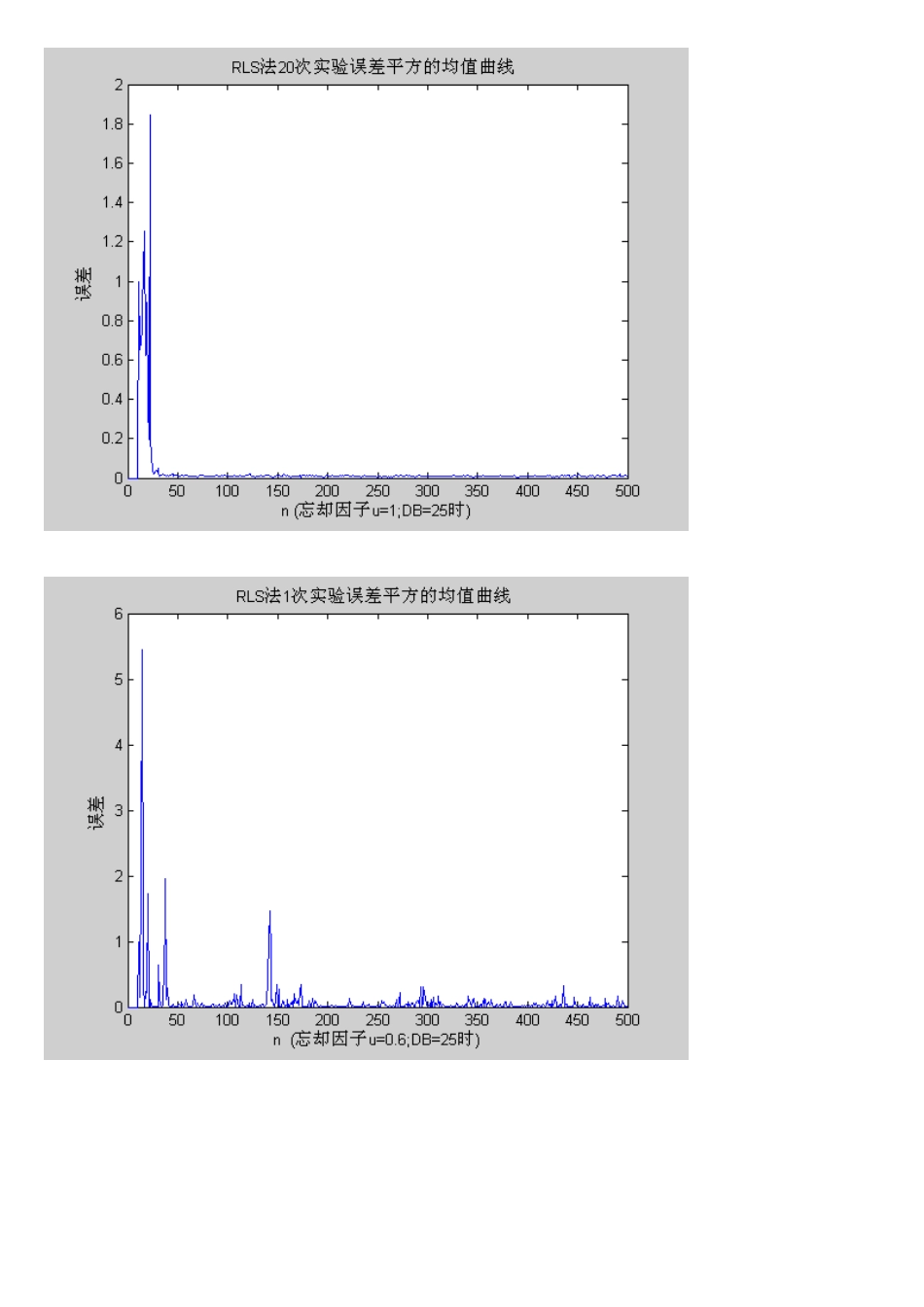
用 RLS 算法实现自适应均衡器的 MATLAB 程序考虑一个线性自适应均衡器的原理方框图如《现代数字信号处理导论》p。275 自适应均衡器应用示意图。随机数据产生双极性的随机序列 x[n],它随机地取+1 和—1.随机信号通过一个信道传输,信道性质可由一个三系数 FIR 滤波器刻画,滤波器系数分别是 0.3,0。9,0。3.在信道输出加入方差为 σ 平方 高斯白噪声,设计一个有 11 个权系数的 FIR 结构的自适应均衡器,令均衡器的期望响应为 x[n-7],选择几个合理的白噪声方差 σ 平方(不同信噪比),进行实验.用 RLS 算法实现这个自适应均衡器,画出一次实验的误差平方的收敛曲线,给出最后设计滤波器系数.一次实验的训练序列长度为 500.进行 20 次独立实验,画出误差平方的收敛曲线.给出 3 个步长值的比较。仿真结果: 用 RLS 算法设计的自适应均衡器系数序号123456789101120次0.0051—0。01180.0290-0.07920.2077—0。54581。4606—0.54050。1926—0。06630。01731次0。0069-0。01570。0265—0。07420.1966-0.53491。4514-0.53930。1987—0.07560。0251 结果分析:可以看到,RLS 算法的收敛速度明显比 LMS 算法快,并且误差也比 LMS 算法小,但是当用更小的忘却因子时,单次实验结果明显变坏,当忘却因子趋于 0 时,LS 算法也就是 LMS 算法。附程序:1。 RLS 法 1 次实验% written in 2025.1.13% written by li***clear;N=500;db=25;sh1=sqrt(10^(—db/10));u=1;m=0。0001*sh1^2;error_s=0;for loop=1:1 w=zeros(1,11)'; p=1/m*eye(11,11); V=sh1*randn(1,N ); Z=randn(1,N)—0。5; x=sign(Z);for n=3:N; M(n)=0。3*x(n)+0.9*x(n-1)+0.3*x(n-2);end z=M+V;for n=8:N; d(n)=x(n—7);endfor n=11:N; z1=[z(n) z(n—1) z(n-2) z(n—3) z(n-4) z(n—5) z(n-6) z(n-7) z(n-8) z(n-9) z(n-10)]'; k=u^(-1)。*p*z1。/(1+u^(—1).*z1’*p*z1); e(n)=d(n)—w’*z1; w=w+k.*conj(e(n)); p=u^(-1)。*p—u^(—1)。*k*z1'*p; y(n)=w’*z1; e1(n)=d(n)—w’*z1;end error_s=error_s+e。^2;endwerror_s=error_s。/1;n=1:N;plot(n,error_s);xlabel(’n (忘却因子 u=1;DB=25 时)’);ylabel('误差’);title('RLS 法 1 次实验误差平方的均值曲线 ’);2. RLS 法 20 次实验% written in 2025.1。13% ...