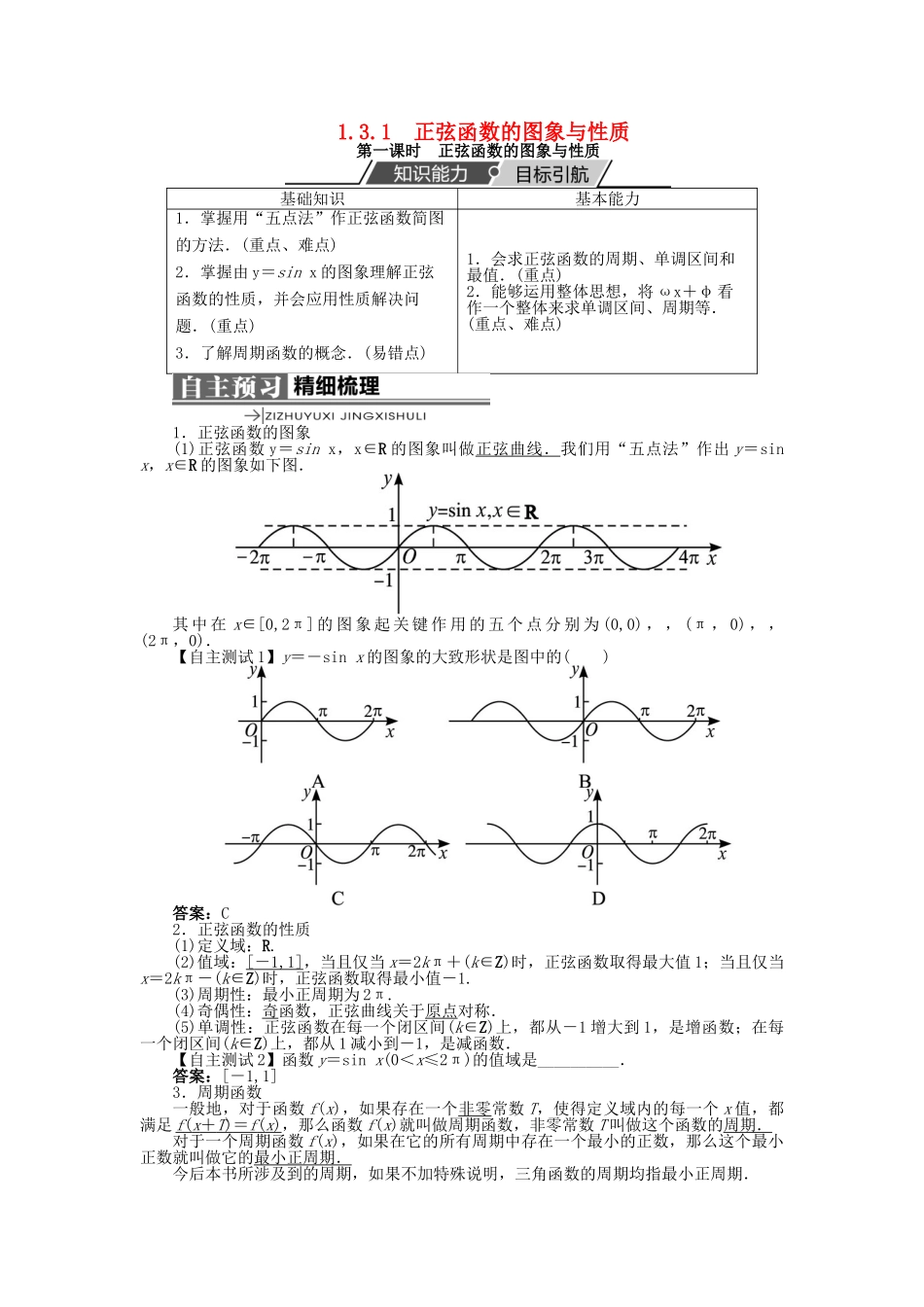
1.3.1 正弦函数的图象与性质第一课时 正弦函数的图象与性质基础知识基本能力1.掌握用“五点法”作正弦函数简图的方法.(重点、难点)2.掌握由 y=sin x 的图象理解正弦函数的性质,并会应用性质解决问题.(重点)3.了解周期函数的概念.(易错点)1.会求正弦函数的周期、单调区间和最值.(重点)2.能够运用整体思想,将 ωx+φ 看作一个整体来求单调区间、周期等.(重点、难点)1.正弦函数的图象(1)正弦函数 y=sin x,x∈R 的图象叫做正弦曲线.我们用“五点法”作出 y=sin x,x∈R 的图象如下图.其 中 在 x∈[0,2π] 的 图 象 起 关 键 作 用 的 五 个 点 分 别 为 (0,0) , , (π , 0) , ,(2π,0).【自主测试 1】y=-sin x 的图象的大致形状是图中的( )答案:C2.正弦函数的性质(1)定义域:R.(2)值域:[ - 1,1] ,当且仅当 x=2kπ+(k∈Z)时,正弦函数取得最大值 1;当且仅当x=2kπ-(k∈Z)时,正弦函数取得最小值-1.(3)周期性:最小正周期为 2π.(4)奇偶性:奇函数,正弦曲线关于原点对称.(5)单调性:正弦函数在每一个闭区间(k∈Z)上,都从-1 增大到 1,是增函数;在每一个闭区间(k∈Z)上,都从 1 减小到-1,是减函数.【自主测试 2】函数 y=sin x(0<x≤2π)的值域是__________.答案:[-1,1]3.周期函数一般地,对于函数 f(x),如果存在一个非零常数 T,使得定义域内的每一个 x 值,都满足 f ( x + T ) = f ( x ) ,那么函数 f(x)就叫做周期函数,非零常数 T 叫做这个函数的周期.对于一个周期函数 f(x),如果在它的所有周期中存在一个最小的正数,那么这个最小正数就叫做它的最小正周期.今后本书所涉及到的周期,如果不加特殊说明,三角函数的周期均指最小正周期.是否所有的周期函数都有最小正周期?请举例说明.答:一个周期函数的周期不止一个,若有最小正周期的话,则最小正周期只有一个,并不是每一个周期函数都有最小正周期,如 f(x)=a(a 为常数)就没有最小正周期.【自主测试 3】f(x)=sin x,x∈R 是( )A.最小正周期为 2π 的偶函数B.最小正周期为 2π 的奇函数C.最小正周期为的偶函数D.最小正周期为的奇函数解析:由正弦函数的性质,可知 f(x)的最小正周期为 2π.又由 f(-x)=sin(-x)=-sin x=-f(x),得 f(x)是奇函数.答案:B1.探讨正弦函数图象的对称性剖析:因为 y=sin x 为奇函数,所以其...