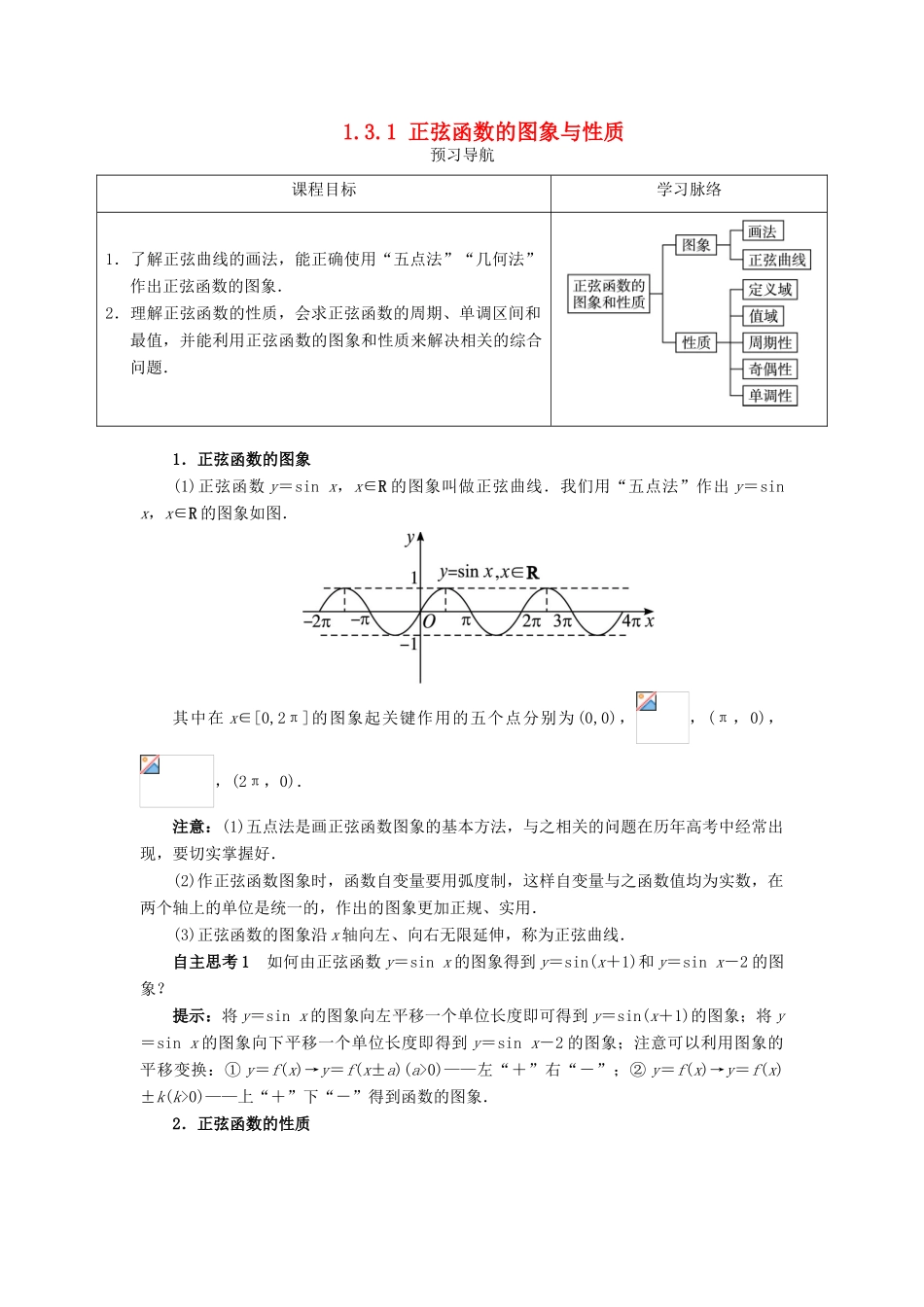
1.3.1 正弦函数的图象与性质预习导航课程目标学习脉络1.了解正弦曲线的画法,能正确使用“五点法”“几何法”作出正弦函数的图象.2.理解正弦函数的性质,会求正弦函数的周期、单调区间和最值,并能利用正弦函数的图象和性质来解决相关的综合问题.1.正弦函数的图象(1)正弦函数 y=sin x,x∈R 的图象叫做正弦曲线.我们用“五点法”作出 y=sin x,x∈R 的图象如图.其中在 x∈[0,2π]的图象起关键作用的五个点分别为 (0,0),,(π,0),,(2π,0).注意:(1)五点法是画正弦函数图象的基本方法,与之相关的问题在历年高考中经常出现,要切实掌握好.(2)作正弦函数图象时,函数自变量要用弧度制,这样自变量与之函数值均为实数,在两个轴上的单位是统一的,作出的图象更加正规、实用.(3)正弦函数的图象沿 x 轴向左、向右无限延伸,称为正弦曲线.自主思考 1 如何由正弦函数 y=sin x 的图象得到 y=sin(x+1)和 y=sin x-2 的图象?提示:将 y=sin x 的图象向左平移一个单位长度即可得到 y=sin(x+1)的图象;将 y=sin x 的图象向下平移一个单位长度即得到 y=sin x-2 的图象;注意可以利用图象的平移变换:① y=f(x)→y=f(x±a)(a>0)——左“+”右“-”;② y=f(x)→y=f(x)±k(k>0)——上“+”下“-”得到函数的图象.2.正弦函数的性质自主思考 2 正弦函数在对称轴和对称中心处的函数值有何特点?提示:(1)正弦曲线的对称轴一定经过正弦曲线的最高点或最低点,此时,正弦函数取最大值或最小值.(2)正弦曲线的对称中心一定是过正弦曲线与 x 轴的交点,即此时的正弦值为 0.自主思考 3 y=sin x,x∈的值域是否是[-1,1]?提示:y=sin x,x∈的值域为[0,1],正弦函数的值域是[-1,1],是指整个正弦曲线或一个周期内的正弦曲线.如果定义域不是全体实数或不在一个周期内,那么正弦函数的值域就可能不是[-1,1].3.周期函数一般地,对于函数 f(x),如果存在一个非零常数 T,使得定义域内的每一个 x 值,都满足 f ( x + T ) = f ( x ) ,那么函数 f(x)就叫做周期函数,非零常数 T 叫做这个函数的周期.对于一个周期函数 f(x),如果在它的所有周期中存在一个最小的正数,那么这个最小正数就叫做它的最小正周期.如果不加特殊说明,三角函数的周期均指最小正周期.归纳总结(1)一个周期函数的周期不止一个,若有最小正周期,则最小正周期只有一个,并不是每一个周期函...