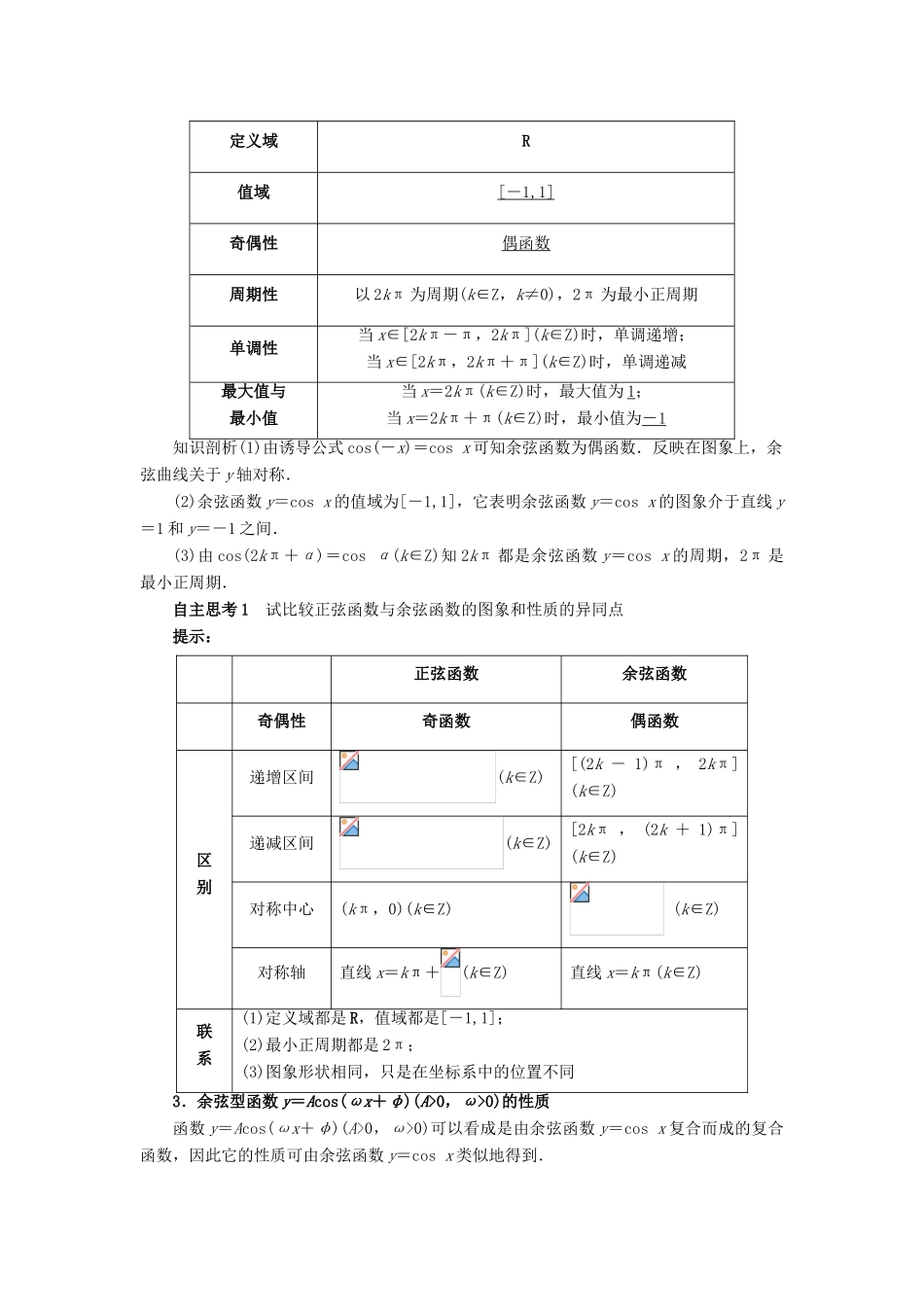
1.3.2 余弦函数、正切函数的图象与性质预习导航课程目标学习脉络1.能正确使用“五点法”“图象变换法”作出余弦函数 y=cos x 和 y=Acos(ωx+φ)的图象,并能体会正弦曲线和余弦曲线的关系.2.理解余弦函数的性质,会求余弦函数的周期、单调区间及最值,并能利用余弦函数的图象和性质来解决相关的综合问题.1.余弦函数图象的画法(1)平移作图:由 y=cos x=sin (x∈R)知,余弦函数 y=cos x 的图象与正弦型函数 y=sin的图象相同.于是把正弦曲线向左平移个单位长度就可得到余弦函数的图象.(2)描点法:按照列表、描点、连线的顺序可以作出余弦函数的图象.(3)几何法:就是利用单位圆中的余弦线来作出余弦函数图象的方法.(4)五点法:函数 y=cos x 在[0,2π]内的图象的五个关键点是(0,1),,(π,-1),,(2π,1),其中,分别是 x 轴上的第一个零点,第二个零点;(0,1),(2π,1),(π,-1)分别是函数图象的第一个最高点,第二个最高点和最低点,描出这五个点后,根据余弦函数的基本形状用光滑曲线将它们连接起来,即可得到[0,2π]内的余弦函数图象.将上述几种作法得到的 y=cos x,x∈[0,2π]的图象向左、右平移(每次 2π 个单位),则可得到 y=cos x,x∈R 的图象,如图所示.2.余弦函数的性质函数y=cos x定义域R值域[ - 1,1] 奇偶性偶函数周期性以 2kπ 为周期(k∈Z,k≠0),2π 为最小正周期单调性当 x∈[2kπ-π,2kπ](k∈Z)时,单调递增;当 x∈[2kπ,2kπ+π](k∈Z)时,单调递减最大值与最小值当 x=2kπ(k∈Z)时,最大值为 1;当 x=2kπ+π(k∈Z)时,最小值为- 1 知识剖析(1)由诱导公式 cos(-x)=cos x 可知余弦函数为偶函数.反映在图象上,余弦曲线关于 y 轴对称.(2)余弦函数 y=cos x 的值域为[-1,1],它表明余弦函数 y=cos x 的图象介于直线 y=1 和 y=-1 之间.(3)由 cos(2kπ+α)=cos α(k∈Z)知 2kπ 都是余弦函数 y=cos x 的周期,2π 是最小正周期.自主思考 1 试比较正弦函数与余弦函数的图象和性质的异同点提示:正弦函数余弦函数奇偶性奇函数偶函数区别递增区间(k∈Z)[(2k - 1)π , 2kπ](k∈Z)递减区间(k∈Z)[2kπ , (2k + 1)π](k∈Z)对称中心(kπ,0)(k∈Z) (k∈Z)对称轴直线 x=kπ+(k∈Z)直线 x=kπ(k∈Z)联系(1)定义域都是 R,值域都是[-1,1];(2)最小正周期都是 2π;(3)图象形状相同,只是在坐标系...