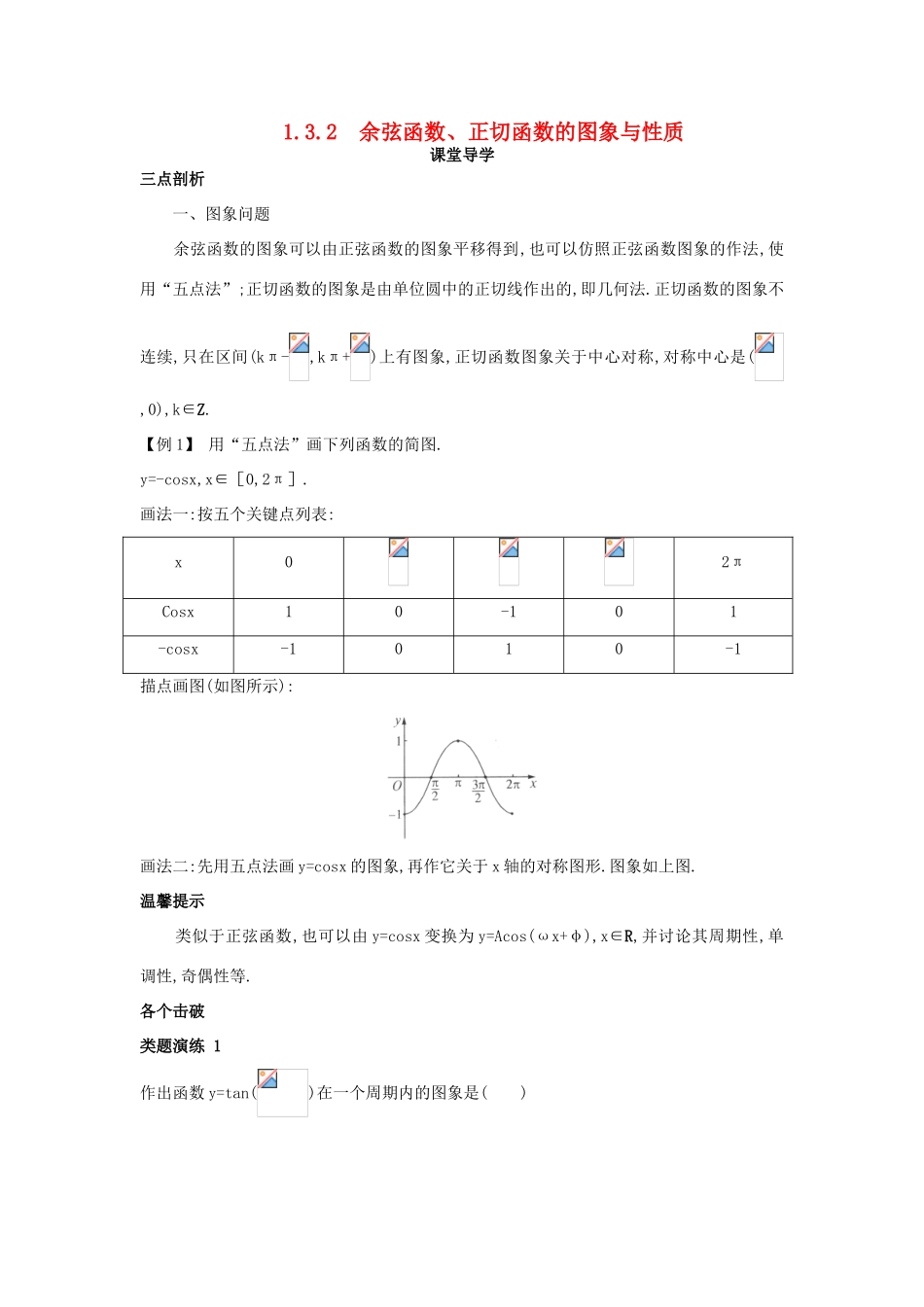
1.3.2 余弦函数、正切函数的图象与性质课堂导学三点剖析 一、图象问题 余弦函数的图象可以由正弦函数的图象平移得到,也可以仿照正弦函数图象的作法,使用“五点法”;正切函数的图象是由单位圆中的正切线作出的,即几何法.正切函数的图象不连续,只在区间(kπ-,kπ+)上有图象,正切函数图象关于中心对称,对称中心是(,0),k∈Z.【例 1】 用“五点法”画下列函数的简图.y=-cosx,x∈[0,2π].画法一:按五个关键点列表:x02πCosx10-101-cosx-1010-1描点画图(如图所示):画法二:先用五点法画 y=cosx 的图象,再作它关于 x 轴的对称图形.图象如上图.温馨提示 类似于正弦函数,也可以由 y=cosx 变换为 y=Acos(ωx+φ),x∈R,并讨论其周期性,单调性,奇偶性等.各个击破类题演练 1作出函数 y=tan()在一个周期内的图象是( )解析:首先函数的周期为 2π,可排除 B,D,其次当 x=时,函数无意义,又可排除 C.答案:A变式提升 1在区间(,)范围内,函数 y=tanx 与函数 y=sinx 的图象交点的个数为( )A.1 B.2 C.3 D.4解法一:在同一坐标系中,首先作出 y=sinx 与 y=tanx 在(-,)内的图象,需明确 x∈(0,)时,有 sinx