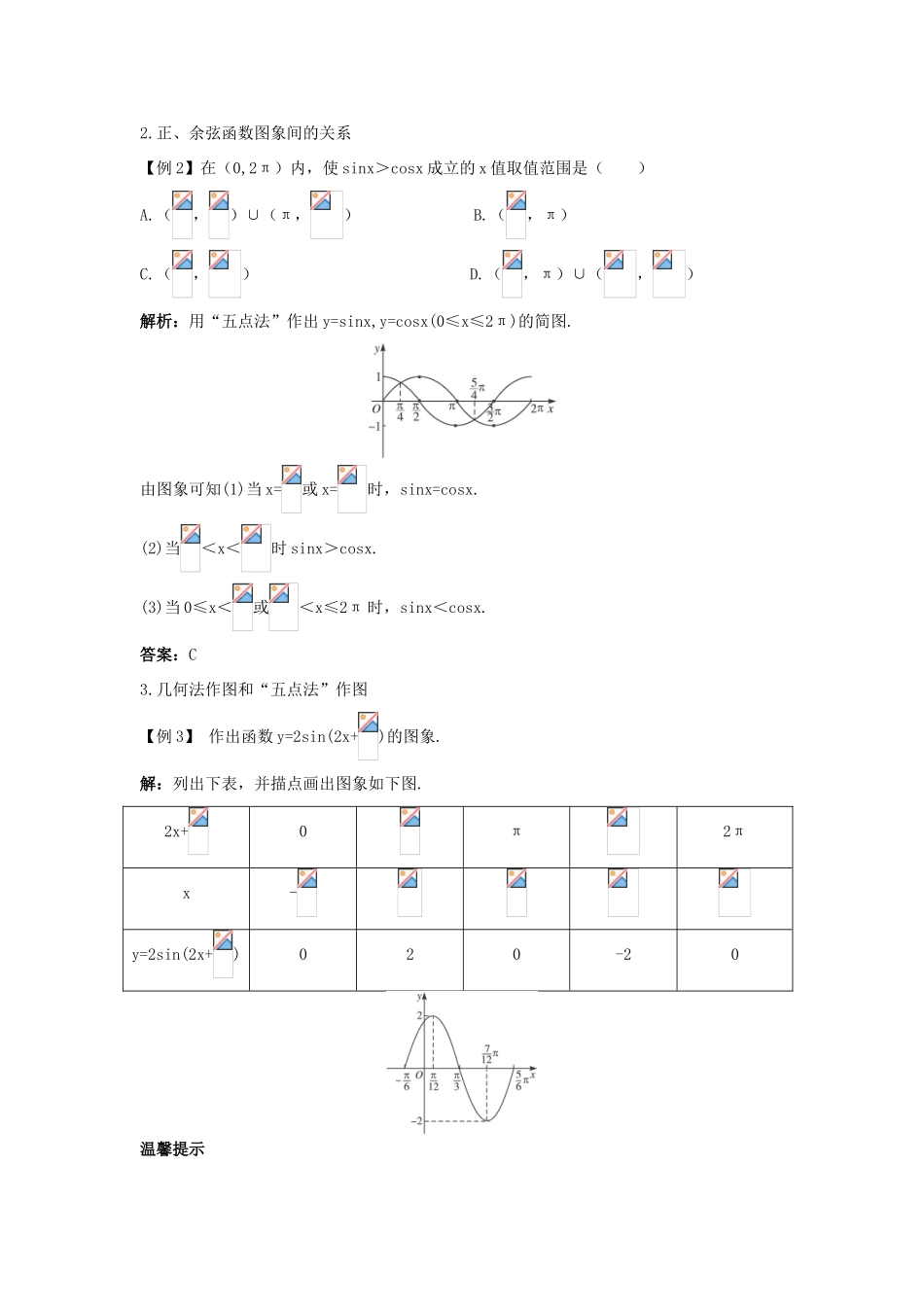
1.4.1 正弦函数、余弦函数的图象课堂导学三点剖析1.正弦函数、余弦函数的图象【例 1】 画下列函数的简图,(1)y=1+cosx,x∈[0,2π];(2)y=-sinx,x∈[0,2π].思路分析:本题主要考查“五点法”作图象.利用“五点法”作图象可分为列表、描点、连线三步.(1)画法:①列表:x0π2πcosx10-1011+cosx21012② 描点:③ 连线:用平滑曲线依次连结各点.(2)画法:①列表:x0π2πsinx010-10-sinx0-1010② 描点:③ 连线:用平滑曲线依次连结各点,即可得到所求图象.温馨提示 一般地 y=f(x)+b 是由 y=f(x)沿 y 轴方向向上(向下)平移|b|个单位得到的. 一般地 y=f(x)与 y=-f(x)的图象关于 x 轴对称.2.正、余弦函数图象间的关系【例 2】在(0,2π)内,使 sinx>cosx 成立的 x 值取值范围是( )A.(,)∪(π,) B.(,π)C.(,) D.(,π)∪(,)解析:用“五点法”作出 y=sinx,y=cosx(0≤x≤2π)的简图.由图象可知(1)当 x=或 x=时,sinx=cosx.(2)当<x<时 sinx>cosx.(3)当 0≤x<或<x≤2π 时,sinx<cosx.答案:C3.几何法作图和“五点法”作图【例 3】 作出函数 y=2sin(2x+)的图象.解:列出下表,并描点画出图象如下图.2x+0π2πx-y=2sin(2x+)020-20温馨提示 “五点法”作图如 y=Asin(ωx+φ)的函数图象时,要从整体的观点找出五个关键点.使式子中 ωx+φ 取 0,,π,,2π,然后求出相应的 x、y 值.各个击破类题演练 1函数 y=1-sinx,x∈[0,2π]的大致图象是( )解析 1:用特殊点代入验证:取(0,1)、(,0)两点检验知 B 正确.解析 2:对于本题可按如下程序进行思考:首 先 作 出 ( 或 想 象 出 ) y=sinx,x∈ [ 0,2π ] 的 图 象 , 然 后 作 出 ( 或 想 象 出 ) y=-sinx,x∈[0,2π]的图象(请同学自己画出);最后作出(或想象出)y=-sinx+1 的图象(请同学自己画出).易得图象就为 B 所示.答案:B变式提升 1作出 y=|sinx|的图象.解:y=(k∈Z)其图象如下图.温馨提示 (1)y=|sinx|的图象可以看作是将 y=sinx 的图象在 x 轴下方的部分翻折到 x 轴的上方得到的.(2)y=|f(x)|的图象是将 y=f(x)的图象在 x 轴下方的部分翻折到 x 轴的上方得到的.类题演练 2要得到函数 f(x)=sinx 的图象,可以将 g(x)=cosx 的图象( )A.向左平移 π 个单位 B.向右平移 π 个单位C.向左平移个单位 D.向右平移个单位解析: y=sinx=cos(+x...