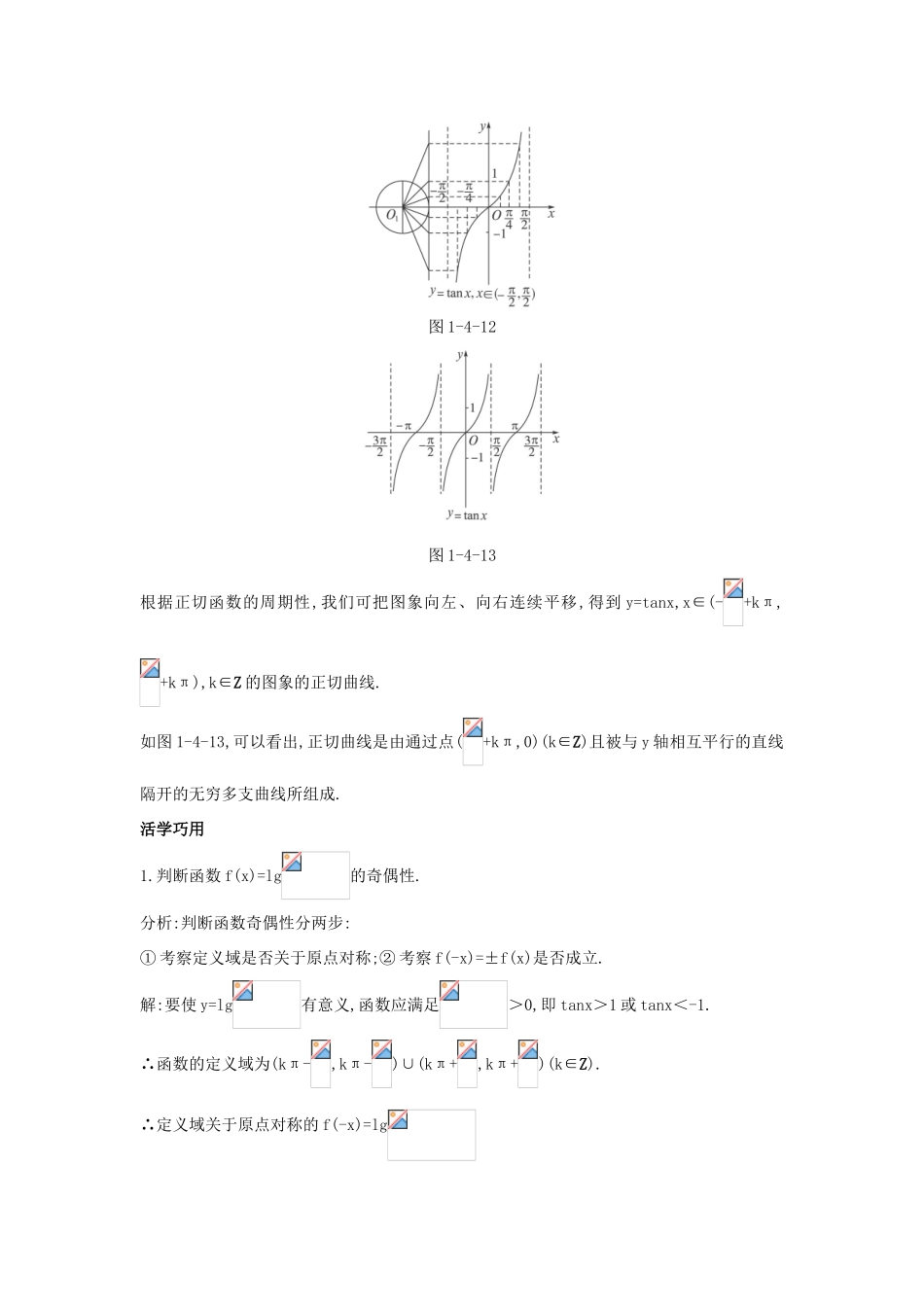
1.4.3 正弦函数、余弦函数的性质互动课堂疏导引导1.正切函数的性质(1)周期性由诱导公式 tan(x+π)=tanx,x∈R,x≠+kπ,k∈Z 可知正切函数是周期函数,周期是 π.(2)奇偶性由诱导公式 tan(-x)=-tanx,x∈R,且 x≠+kπ,k∈Z,可知正切函数是奇函数.(3)单调性如图 1-4-11(1)(2),由正切函数线的变化规律得,正切函数在(-,)内是增函数,又由周期性可知正切函数在开区间(-+kπ, +kπ),k∈Z 内都是增函数.图 1-4-11(4)值域如图 1-4-11(1),当 x 大于-且无限接近-时,正切线 AT 向 Ov 轴的负方向无限延伸;如图1-4-11(2),当 x 小于且无限接近时,正切线 AT 向 Ov 轴的正方向无限延伸.因此,tanx在(-,)内可取任意实数,但没有最大值、最小值.2.正切函数的图象 正切函数的图象的画法与正弦函数图象的画法类似,正切函数的图象是利用单位圆上的正切线来作的.如图 1-4-12.图 1-4-12图 1-4-13根据正切函数的周期性,我们可把图象向左、向右连续平移,得到 y=tanx,x∈(-+kπ, +kπ),k∈Z 的图象的正切曲线.如图 1-4-13,可以看出,正切曲线是由通过点(+kπ,0)(k∈Z)且被与 y 轴相互平行的直线隔开的无穷多支曲线所组成.活学巧用1.判断函数 f(x)=lg的奇偶性.分析:判断函数奇偶性分两步:① 考察定义域是否关于原点对称;② 考察 f(-x)=±f(x)是否成立.解:要使 y=lg有意义,函数应满足>0,即 tanx>1 或 tanx<-1.∴函数的定义域为(kπ-,kπ-)∪(kπ+,kπ+)(k∈Z).∴定义域关于原点对称的 f(-x)=lg==-f(x).∴y=是奇函数.2.已知函数 y=tan(2x+φ)的图象过点(,0),则 y 可以是( )A.- B. C.- D.解析:∵y=tan(2x+φ)过(,0),∴tan(+φ)=0.∴+φ=kπ.∴φ=kπ-.∴k=0 时,φ=-.答案:A3.根据正切函数的图象,写出下列不等式的解集.(1)tanx≥-1;(2)tan2x≤-1.解析:作出 y=tanx 的图象,如图 1-4-14.图 1-4-14(1)∵tanx≥-1,tan(-)=-1,在(-,)内,满足条件的 x 为-≤x<,由正切函数的图象,可知满足此不等式的 x 的集合为{x|-+kπ≤x<+kπ,k∈Z}.(2)在(-,)内,tan(-)=-1,∴不等式的解集由不等式 kπ-<2x≤kπ- (k∈Z)确定.解得-<x≤k- (k∈Z).∴不等式 tan2x≤-1 的解集为{x|-<x≤-,k∈Z}.答案:(1){x|-+kπ≤x<+kπ,k∈Z};(2){x|-<x≤-,k∈Z}.