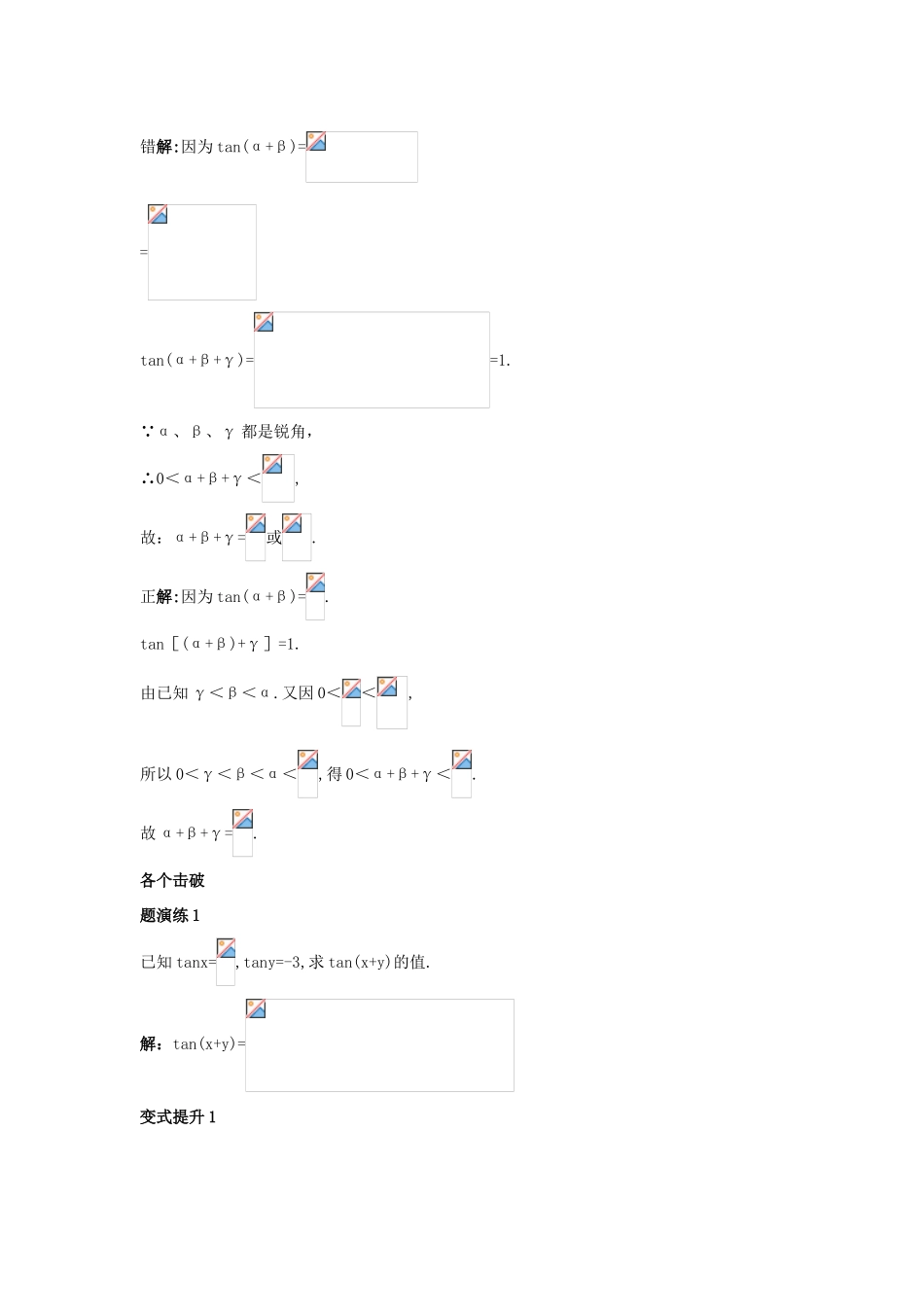
3.1.3 二倍角的正弦、余弦、正切公式(2)课堂导学三点剖析1.两角和与差的正切【例 1】 已知 tan(α+β)=5,tan(α-β)=3,求 tan2α,tan2β,tan(2α+).思路分析:想办法利用已知条件中的角 α+β 与 α-β 表示所求式中的角,不难看出2α=(α+β)+(α-β),2β=(α+β)-(α-β),tan(2α+)用 tan2α 表示出来.解:tan2α=tan[(α+β)+(α-β)]=tan2β=tan[(α+β)-(α-β)]=tan(2α+)=.2.两角和与差的正切公式的运用【例 2】计算下列各式的值:(1)tan15°+tan75°;(2);(3);(4);(5)解:(1)tan15°+tan75°=tan(45°-30°)+tan(45°+30°)=====2-+2+=4;(2)原式==tan(45°-15°)=tan30°=;(3)原式=tan(41°+19°)=tan60°=;(4)原式=tan[(α+)-(α+)]=tan=;(5)原式==tan(-)=tan=1.3.给值求角问题【例 3】 已知 α,β,γ 都是锐角,且 tanα=,tanβ=,tanγ=,求 α+β+γ 的值.错解:因为 tan(α+β)==tan(α+β+γ)==1.∵α、β、γ 都是锐角,∴0<α+β+γ<,故:α+β+γ=或.正解:因为 tan(α+β)=.tan[(α+β)+γ]=1.由已知 γ<β<α.又因 0<<,所以 0<γ<β<α<,得 0<α+β+γ<.故 α+β+γ=.各个击破题演练 1已知 tanx=,tany=-3,求 tan(x+y)的值.解:tan(x+y)=变式提升 1已知 tanα=,tanβ=,求 tan(α+2β).解:tan(α+β)=,tan(α+2β)=tan[(α+β)+β]==1.类题演练 2利用和(差)角公式化简:(1);(2).解:(1)原式=tan(2θ-θ)=tanθ.(2)原式==tan(-θ).变式提升 2 (1)求 tan50°-tan20°-tan50·tan20°的值.解∵tan50°-tan20°=tan30°(1+tan50°·tan20°),∴tan50°-tan20°-tan50°·tan20°=tan30°(1+tan50°tan20°)-tan50°·tan20°=tan30°+tan30°·tan50°tan20°-tan50°·tan20°=tan30°=.(2)化简:tan(18°-x)tan(12°+x)+[tan(18°-x)+tan(12°+x)]解:tan30°=tan[(18°-x)+(12°+x)]=.∴tan(18°-x)+tan(12°+x)=[1-tan(18°-x)tan(12°+x)].∴原式=1.温馨提示 tanα±tanβ=tan(α±β)(1tanαtanβ)这一公式变形在解题中经常用到,只要题目中有 tanα+tanβ 或 tanα-tanβ,一般用正切公式的变形,整体代入都能凑效.类题演练 3已知 α、β 都是锐角,且 tanα=,tanβ=,求 α+β.解:tan(α+β)==∵α、β 均为锐角,∴0°<α+β<180°∴α+β=45°.变式提升 3已知 tanα=(1+m),(tanα·tanβ+m)+tanβ=0,且 α、β 都是锐角,求 α+β.解:由已知可得tanα=+m,①tanβ=-tanαtanβ-m.②由①+② 可得tanα+tanβ=(1-tanαtanβ),∴=tan(α+β)=.又∵0<α<,0<β<,∴0<α+β<π,∴α+β=.