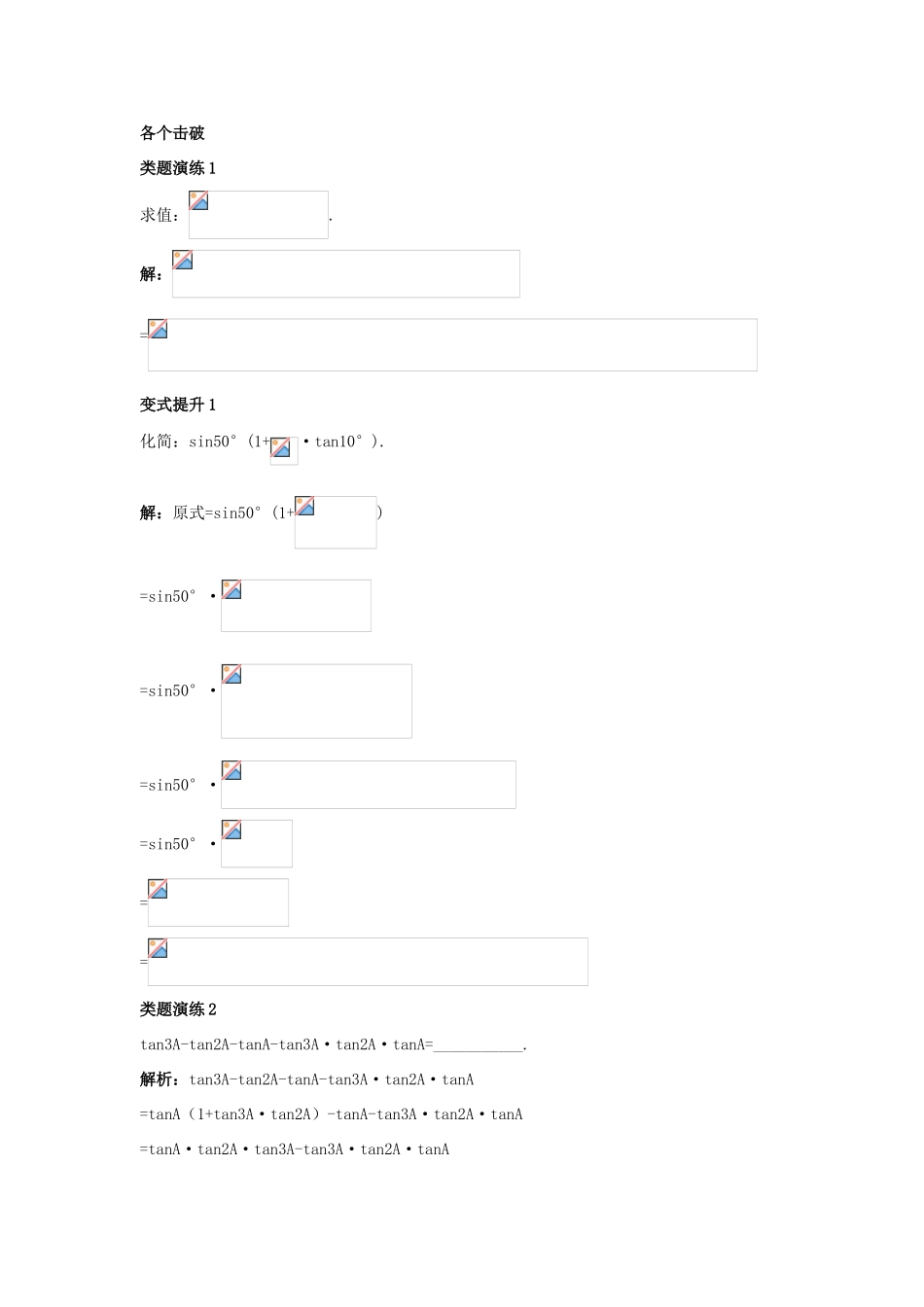
3.1.3 二倍角的正弦、余弦、正切公式(3)课堂导学三点剖析1.运用两角和与差的正弦、余弦、正切公式进行化简,求值和证明【例 1】求值:(tan10°-)·解法 1:(tan10°-)=(tan10°-tan60°)=()==解法 2:(tan10°-)=(tan10°-tan60°)=tan(10°-60°)(1+tan10°tan60°)=-tan50°(1+tan10°·tan60°)=-tan50°(1+sin10°·)=温馨提示(1)在给角问题中,既有弦函数又有切函数的往往将切函数化为弦函数;(2)在给角求值问题中应首先观察角之间的关系,要根据减元的思想即尽量减少一般角的个数.2.两角和与差的正弦、余弦、正切公式的灵活运用【例 2】 化简:3sin(x+20°)-5sin(x+80°)+cos(x+20°)思路分析:注意到式子中涉及的两角 x+80°与 x+20°之差为 60°,是特殊角,进行变换化简.解:原式=3sin(x+20°)-5sin[(x+20°)+60°]+cos(x+20°)=3sin(x+20°)-5sin(x+20°)cos60°-5cos(x+20°)sin60°+23cos(x+20°)=sin(x+20°)-cos(x+20°)=sin(x+20°)cos60°-cos(x+20°)sin60°=sin(x+20°-60°)=sin(x-40°)温馨提示 对公式的灵活运用,主要从整体结构入手.还要特别注意角的联系及三角函数的名称.3.注意角与角之间的联系,从整体入手解决问题【例 3】 化简:sin(α+β)cosα-[sin(2α+β)-sinβ].思路分析:本题中出现 α+β,α,2α+β,β 四个角,为尽量减少角的个数,可以将2α+β,表示成(α+β)+α,将 β 表示成(α+β)-α,然后再利用两角差和的正余弦公式便可获解.解:sin(α+β)cosα-[sin(2α+β)-sinβ]=sin(α+β)cosα-[sin(α+β+α)-sin(α+β-α)]=sin ( α+β ) cosα-[ sin ( α+β ) cosα+cos ( α+β ) sinα-sin(α+β)cosα+cos(α+β)sinα]=sin(α+β)cosα-cos(α+β)sinα=sin(α+β-α)=sinβ.温馨提示 本题仍是抓住题目中角之间的联系,利用角的变换将 2α+β 表示成(α+β)+α,将β 表示成(α+β)-α.不要盲目的展成单角 α 与 β 的三角函数,那将会使题目变得相当复杂.各个击破类题演练 1求值:.解:=变式提升 1化简:sin50°(1+·tan10°).解:原式=sin50°(1+)=sin50°·=sin50°·=sin50°·=sin50°·==类题演练 2tan3A-tan2A-tanA-tan3A·tan2A·tanA=___________.解析:tan3A-tan2A-tanA-tan3A·tan2A·tanA=tanA(1+tan3A·tan2A)-tanA-tan3A·tan2A·tanA...