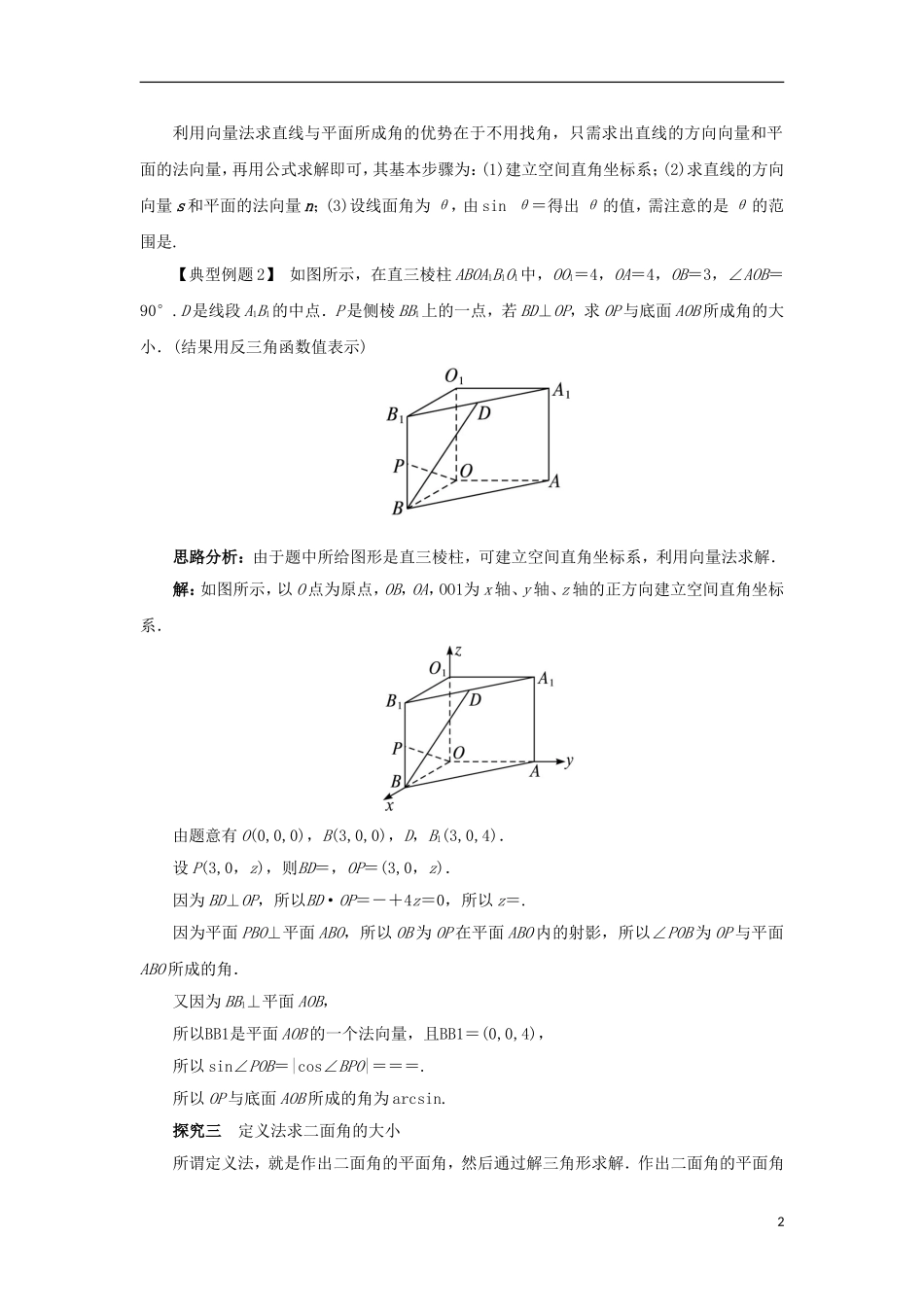
3.2.3 直线与平面的夹角 3.2.4 二面角及其度量课堂探究探究一 用定义法求直线与平面所成的角利用定义法求直线与平面所成的角,首先要作出斜线和这条斜线在平面内的射影所成的锐角,然后通过解三角形求出直线与平面所成的角的大小.其基本步骤可归纳为“一作,二证,三计算”.【典型例题 1】 在正四面体 ABCD 中,E 为棱 AD 的中点,连接 CE,求 CE 和平面 BCD 所成角的正弦值.思路分析:在求解斜线和平面所成的角时,确定斜线在平面内的射影的位置是一个既基本又重要的问题.解:如图,过 A,E 分别作 AO⊥平面 BCD,EG⊥平面 BCD,O,G 为垂足.则 AO∥GE,AO=2GE.连接 GC,则∠ECG 为 EC 和平面 BCD 所成的角.因为 AB=AC=AD,所以 OB=OC=OD.因为△BCD 是正三角形,所以 O 为△BCD 的中心.连接 DO 并延长交 BC 于 F,则 F 为 BC 的中点.令正四面体 ABCD 的棱长为 1,可求得 CE=,DF=,OD=,则 AO===,所以 EG=.在 Rt△ECG 中,sin∠ECG==.归纳找射影的两种方法:(1)斜线上任一点在平面内的射影必在斜线在平面内的射影上;(2)利用已知垂直关系得出线面垂直,确定射影.探究二 向量法求直线与平面所成的角1利用向量法求直线与平面所成角的优势在于不用找角,只需求出直线的方向向量和平面的法向量,再用公式求解即可,其基本步骤为:(1)建立空间直角坐标系;(2)求直线的方向向量 s 和平面的法向量 n;(3)设线面角为 θ,由 sin θ=得出 θ 的值,需注意的是 θ 的范围是.【典型例题 2】 如图所示,在直三棱柱 ABOA1B1O1中,OO1=4,OA=4,OB=3,∠AOB=90°.D 是线段 A1B1的中点.P 是侧棱 BB1上的一点,若 BD⊥OP,求 OP 与底面 AOB 所成角的大小.(结果用反三角函数值表示)思路分析:由于题中所给图形是直三棱柱,可建立空间直角坐标系,利用向量法求解.解:如图所示,以 O 点为原点,OB,OA,OO1为 x 轴、y 轴、z 轴的正方向建立空间直角坐标系.由题意有 O(0,0,0),B(3,0,0),D,B1(3,0,4).设 P(3,0,z),则BD=,OP=(3,0,z).因为 BD⊥OP,所以BD·OP=-+4z=0,所以 z=.因为平面 PBO⊥平面 ABO,所以 OB 为 OP 在平面 ABO 内的射影,所以∠POB 为 OP 与平面ABO 所成的角.又因为 BB1⊥平面 AOB,所以BB1是平面 AOB 的一个法向量,且BB1=(0,0,4),所以 sin∠POB=|cos∠BPO|===.所以 OP 与底面 A...