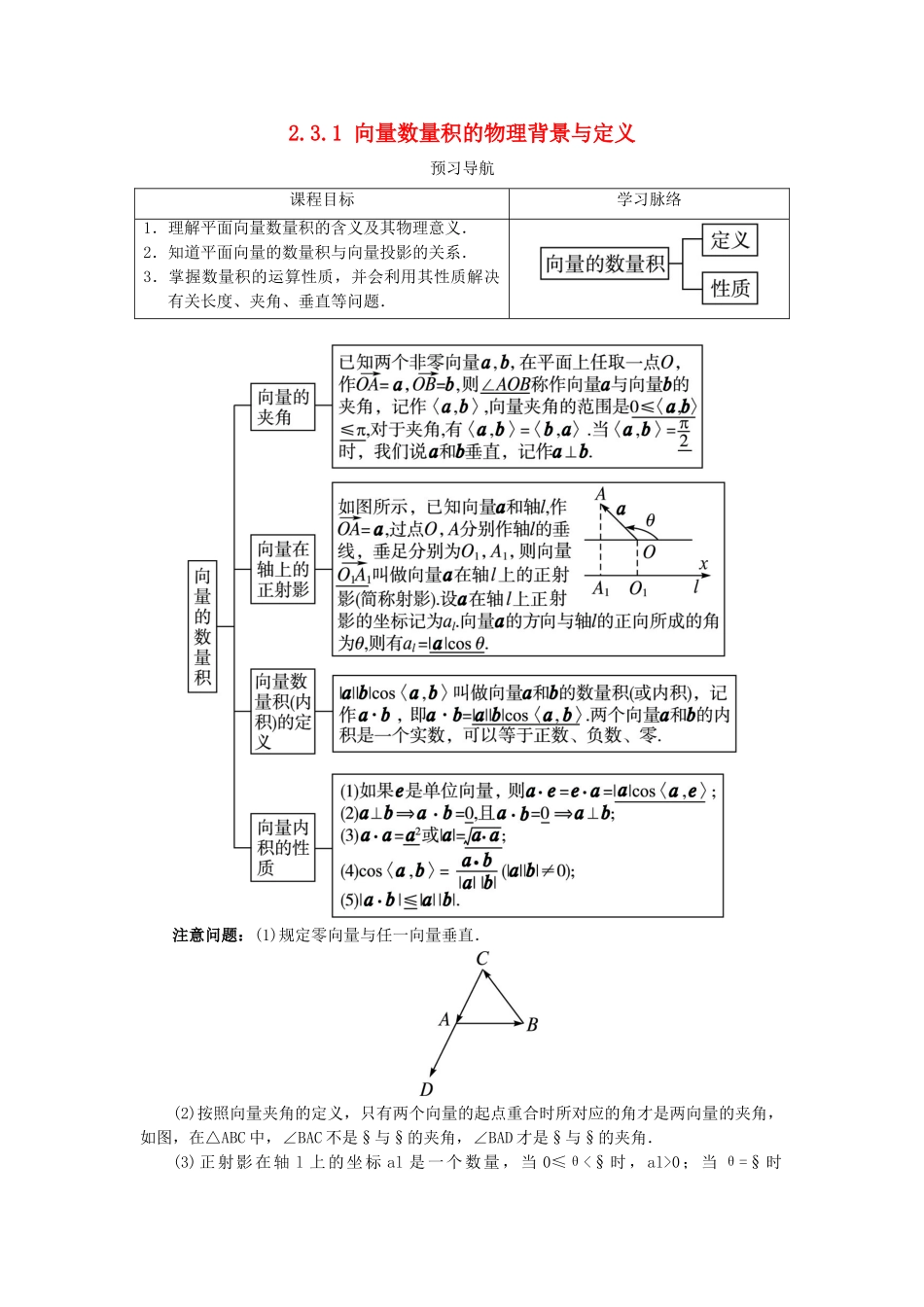
2.3.1 向量数量积的物理背景与定义预习导航课程目标学习脉络1.理解平面向量数量积的含义及其物理意义.2.知道平面向量的数量积与向量投影的关系.3.掌握数量积的运算性质,并会利用其性质解决有关长度、夹角、垂直等问题.注意问题:(1)规定零向量与任一向量垂直.(2)按照向量夹角的定义,只有两个向量的起点重合时所对应的角才是两向量的夹角,如图,在△ABC 中,∠BAC 不是§与§的夹角,∠BAD 才是§与§的夹角.(3)正射影在轴 l 上的坐标 al 是一个数量,当 0≤θ<§时,al>0;当 θ=§时al=0;当§<θ≤π 时,al<0.(4)两向量的数量积,其结果是个数量,而不是向量,它的值为两向量的模与两向量夹角的余弦的乘积,其符号由夹角的余弦值决定.(5)两个向量的数量积是两个向量之间的一种乘法,与以前学过的数的乘法是有区别的,在书写时一定要把它们严格区分开来,绝不可混淆.(6)在运用数量积公式解题时,一定要注意两向量夹角的范围是 0°≤θ≤180°.注意三种特殊情况:当 θ=0°时,a 与 b 同向;当 θ=90°时,a⊥b;当 θ=180°时,a 与 b反 向 . 当 0°≤θ<90° 时 , a·b>0 ; 当 θ=90° 时 , a·b=0 ; 当 90°<θ≤180° 时 ,a·b<0.(7)若 a≠0,由 a·b=0 不能推出 b 一定是零向量,因为当 a⊥b(b≠0)时,a·b=0.自主思考 向量的数量积、向量的数乘和实数的乘法,这三种运算在定义和表示方法上有何区别?提示:(1)从定义上看:两个向量的数量积的结果是一个实数,而不是向量,符号由夹角的大小决定;向量的数乘的结果是一个向量,其长度是原向量长度的倍数,其方向由这个实数的符号决定;两个实数的积是一个实数,符号由这两个实数的符号决定.(2)从运算的表示方法上看:两个向量 a,b 的数量积称为内积,写成 a·b,符号“·”在向量运算中不是乘号,既不能省略,也不能用“×”代替;向量的数乘的写法同单项式的写法;实数的乘法的写法我们就非常熟悉了.