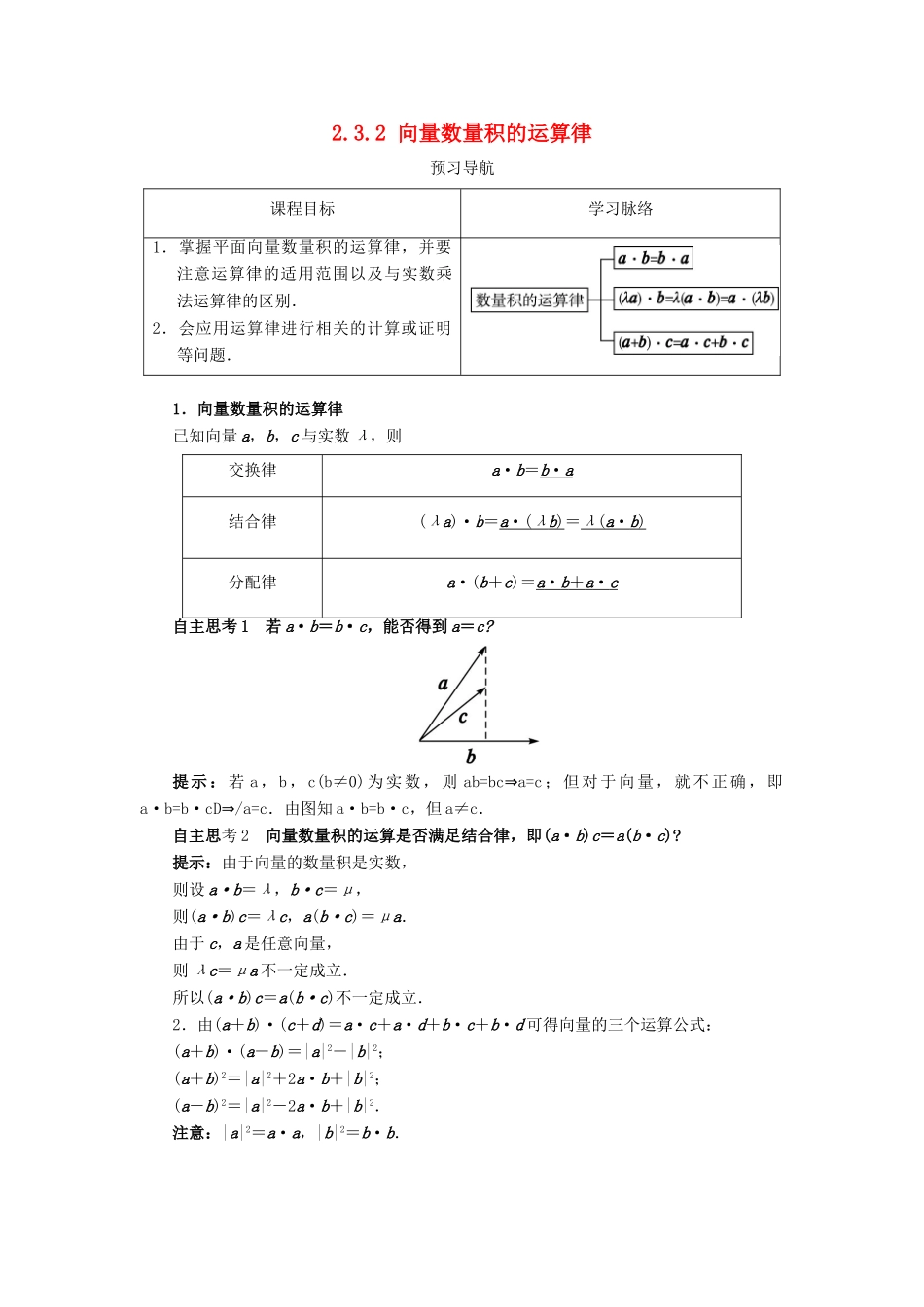
2.3.2 向量数量积的运算律预习导航课程目标学习脉络1.掌握平面向量数量积的运算律,并要注意运算律的适用范围以及与实数乘法运算律的区别.2.会应用运算律进行相关的计算或证明等问题.1.向量数量积的运算律已知向量 a,b,c 与实数 λ,则交换律a·b=b · a 结合律(λa)·b=a ·( λ b ) =λ ( a · b ) 分配律a·(b+c)=a · b + a · c 自主思考 1 若 a·b=b·c,能否得到 a=c?提示:若 a,b,c(b≠0)为实数,则 ab=bc⇒a=c;但对于向量,就不正确,即a·b=b·cD⇒/a=c.由图知 a·b=b·c,但 a≠c.自主思考 2 向量数量积的运算是否满足结合律,即(a·b)c=a(b·c)?提示:由于向量的数量积是实数,则设 a·b=λ,b·c=μ,则(a·b)c=λc,a(b·c)=μa.由于 c,a 是任意向量,则 λc=μa 不一定成立.所以(a·b)c=a(b·c)不一定成立.2.由(a+b)·(c+d)=a·c+a·d+b·c+b·d 可得向量的三个运算公式:(a+b)·(a-b)=|a|2-|b|2;(a+b)2=|a|2+2a·b+|b|2;(a-b)2=|a|2-2a·b+|b|2.注意:|a|2=a·a,|b|2=b·b.