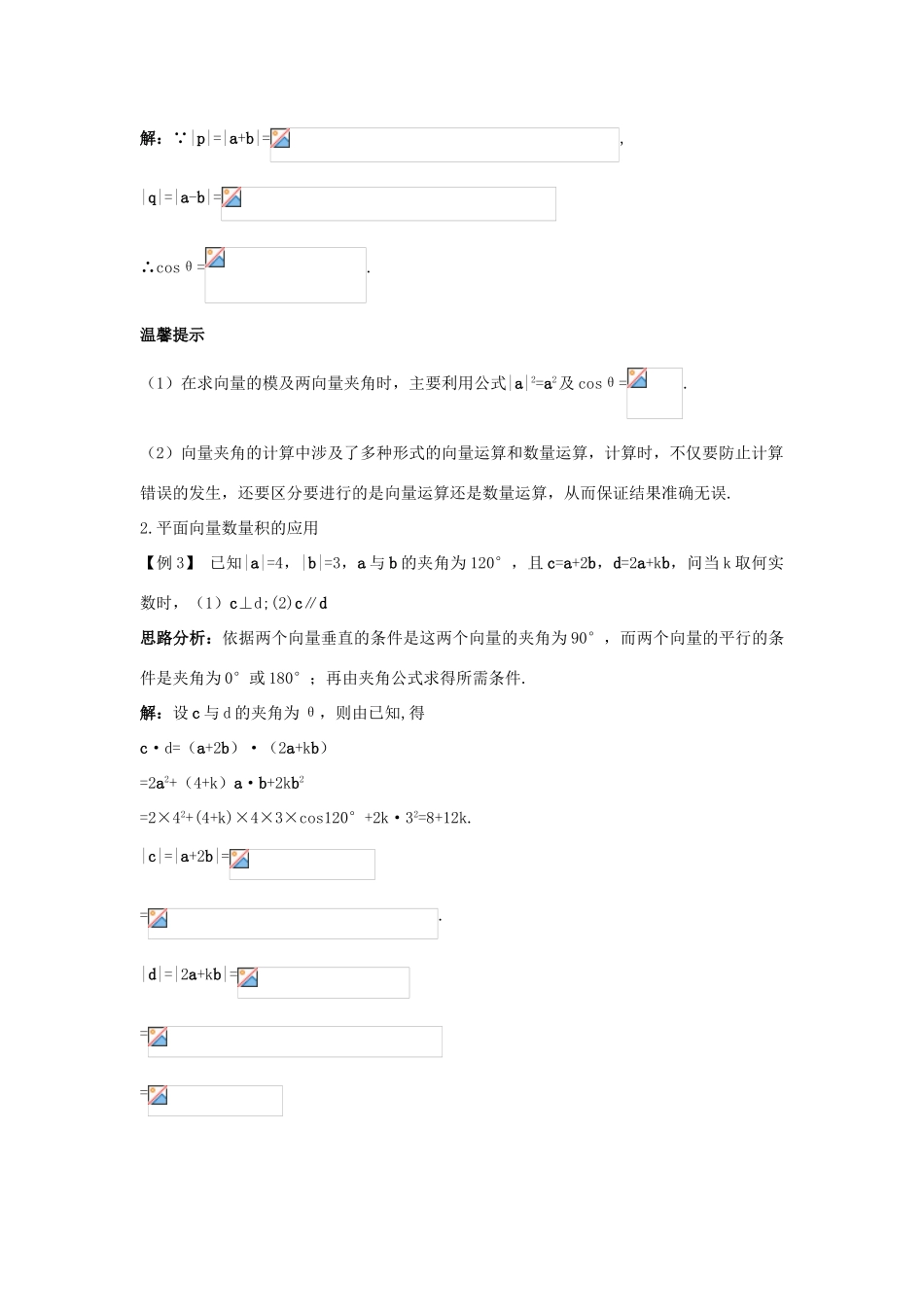
2.4.1 平面向量数量积的物理背景及其含义课堂导学课堂导学1.平面向量数量积的概念【例 1】 已知|a|=5,|b|=4,a 与 b 的夹角为 120°,求:(1)a·b;(2)(a+b)2;(3)a2-b2;(4)(2a-b)·(a+3b).思路分析:由于向量的数量积满足乘法对加法的分配律,因此向量的数量积运算可类似于多 项 式 的 乘 法 运 算 , 如 ( a+b ) 2= ( a+b ) · ( a+b ) = ( a+b ) ·a+(a+b)·b=a·a+b·a+a·b+b·b= a2+2a·b+b2.解:(1)a·b=|a||b|cos120°=5×4×(-)=-10.(2)(a+b)2=a2+2a·b+b2=|a|2+2a·b+|b|2=25-2×10+16=21.(3)a2-b2=|a|2-|b|2=25-16=9.(4)(2a-b)·(a+3b)=2a2+5a·b-3b2=2|a|2+5a·b-3|b|2=2×25+5×(-10)-3×16=-48.温馨提示(1)在进行向量数量积运算时,要严格按运算律进行;(2)由于向量数量积满足乘法对加法的分配律,故向量数量积中也有类似多项式乘法的公式:(a±b)2=a2±2a·b+b2,(a+b)·(a-b)=a2-b2(a+b+c)2=a2+b2+c2+2a·b+2b·c+2a·c.【例 2】已知 a 与 b 的夹角为 30°,且|a|=,|b|=1,求向量 p=a+b 与 q=a-b 的夹角的余弦.思路分析:利用 cosθ=确定 p,q 的夹角,必先求 pq 及|p||q|,而求|p|及|q|利用模长公式|p|2=p2,|q|2=q2.解: |p|=|a+b|=,|q|=|a-b|=∴cosθ=.温馨提示(1)在求向量的模及两向量夹角时,主要利用公式|a|2=a2及 cosθ=.(2)向量夹角的计算中涉及了多种形式的向量运算和数量运算,计算时,不仅要防止计算错误的发生,还要区分要进行的是向量运算还是数量运算,从而保证结果准确无误.2.平面向量数量积的应用【例 3】 已知|a|=4,|b|=3,a 与 b 的夹角为 120°,且 c=a+2b,d=2a+kb,问当 k 取何实数时,(1)c⊥d;(2)c∥d思路分析:依据两个向量垂直的条件是这两个向量的夹角为 90°,而两个向量的平行的条件是夹角为 0°或 180°;再由夹角公式求得所需条件.解:设 c 与 d 的夹角为 θ,则由已知,得c·d=(a+2b)·(2a+kb)=2a2+(4+k)a·b+2kb2=2×42+(4+k)×4×3×cos120°+2k·32=8+12k.|c|=|a+2b|==.|d|=|2a+kb|===∴cosθ=(1)要使 c⊥d,只要 cosθ=0,即 6k+4=0,∴k=-.(2)要使 c∥d,只需 cosθ=±1,即=±(6k+4),解得 k=4.综上,当 k=-时,c⊥d;当 k=4 时,c∥d.温馨提示两向量平行,夹角为 0°或 180°,故有 a·b=|a||b|或 a·b=-|a||b|.而两向量垂直,夹角为 90°,所以 a·...