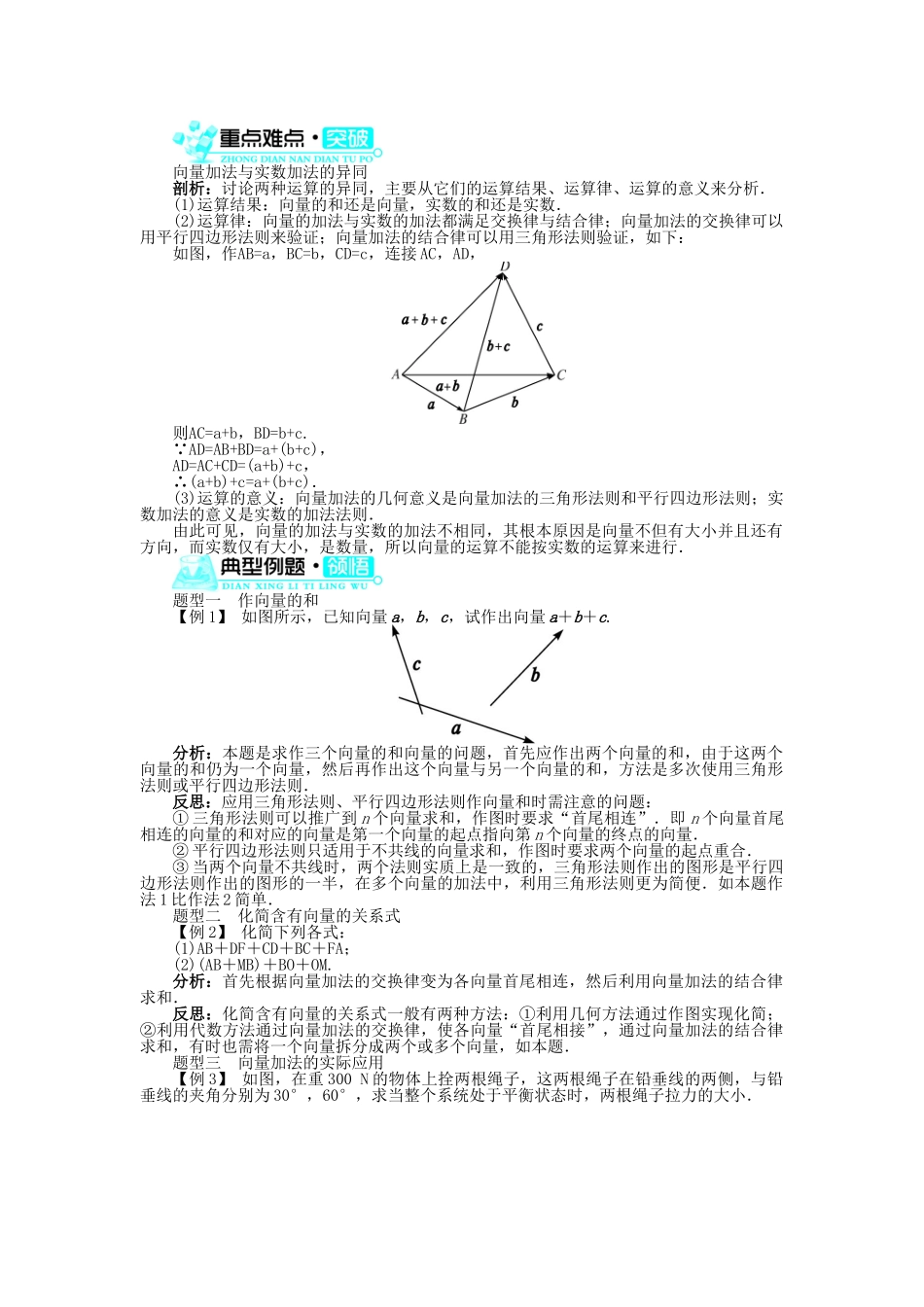
2.2.1 向量加法运算及其几何意义1.通过位移、力的合成了解向量加法定义的由来.2.掌握向量加法的定义,会用向量加法的三角形法则和平行四边形法则作两个向量的和向量.3.掌握向量加法的交换律和结合律,并会用它们进行向量计算,初步掌握向量加法的实际应用.1.向量的加法(1)定义:求两个向量____的运算,叫做向量的加法.两个向量的和仍然是一个______.(2)三角形法则:如图甲所示,已知非零向量 a,b,在平面内任取一点 A,作AB=a,BC=b,则向量______叫做向量 a 与 b 的和,记作 a+b.这种求______的方法叫做向量加法的三角形法则.(3)平行四边形法则:已知两个不共线向量 a,b(如图乙所示),作AB=a,AD=b,则A,B,D 三点不共线,以AB,AD为邻边作平行四边形 ABCD,则向量______=a+b,这种作两个向量和的方法叫做向量加法的平行四边形法则.① 向量加法的多边形法则:n 个向量经过平移,顺次使前一个向量的终点与后一个向量的起点重合,组成一组向量折线,这 n 个向量的和等于折线起点到终点的向量.这个法则叫做向量加法的多边形法则.多边形法则实质就是三角形法则的连续应用.② 三角形法则和平行四边形法则就是向量加法的几何意义.(4)规定:a+0=0+a=a.(5)结论:|a+b|≤|a|+|b|.【做一做 1-1】 AB+BD等于( )A.AB B.BD C.AD D.DA【做一做 1-2】 在平行四边形 ABCD 中,AB+AD等于( )A.ACB.BC C.CD D.BD【做一做 1-3】 在边长为 1 的正方形 ABCD 中,|AB+BC+CD|等于( )A.0 B.1 C. D.32.向量加法的运算律交换律a+b=________结合律(a+b)+c=________【做一做 2】 化简PB+OP+BO=__________.答案:1.(1)和 向量 (2)AC 向量和 (3)AC【做一做 1-1】 C【做一做 1-2】 A【做一做 1-3】 B |AB+BC+CD|=|AC+CD|=|AD|=1.2.b+a a+(b+c)【做一做 2】 0 PB+OP+BO=(OP+PB)+BO=OB+BO=0.向量加法与实数加法的异同剖析:讨论两种运算的异同,主要从它们的运算结果、运算律、运算的意义来分析.(1)运算结果:向量的和还是向量,实数的和还是实数.(2)运算律:向量的加法与实数的加法都满足交换律与结合律;向量加法的交换律可以用平行四边形法则来验证;向量加法的结合律可以用三角形法则验证,如下:如图,作AB=a,BC=b,CD=c,连接 AC,AD,则AC=a+b,BD=b+c. AD=AB+BD=a+(b+c),AD=AC+CD=(a+b)+c,∴(a+b)+c=a+(b+c).(3)运算的意义:向...