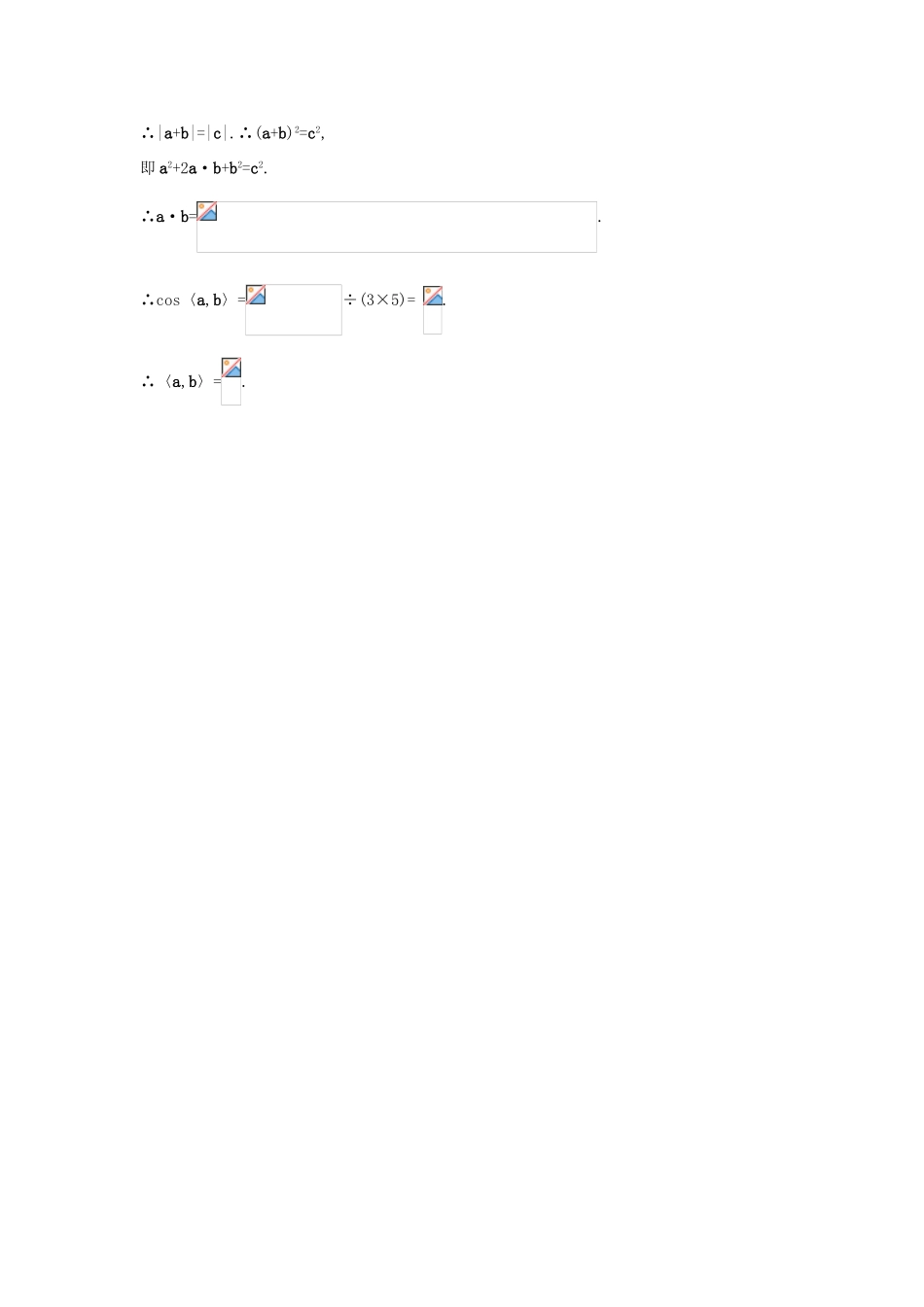
2.4.2 平面向量数量积的坐标表示、模、夹角互动课堂疏导引导1.向量内积的坐标运算建 立 正 交 基 底 {e1,e2}, 已 知 a=(a1,a2),b=(b1,b2), 则 a·b=(a1e1+a2e2)(b1e1+b2e2)=a1b1e12+ (a1b2+a2b1)·e1·e2+a2b2e22.因为 e1·e1=e2·e2=1,e1·e2=e2·e1=0,故 a·b=a1b1+a2b2.疑难疏引(1)两个向量的数量积等于它们对应的坐标的乘积的和,并且此式是在正交基底{e1,e2}下实现的.(2)引入坐标后,实现了向量的数量积和向量坐标间运算的转化.2. 用 向 量 的 坐 标 表 示 两 个 向 量 垂 直 的 条 件 , 设 a=(a1,a2),b=(b1,b2), 如 果 a⊥b, 则a1b1+a2b2=0,反之,若 a1b1+a2b2=0,则 a⊥b.当 a⊥b 时,若 b1b2≠0,则向量(a1,a2)与(-b2,b1)平行,这是因为 a⊥b,a1b1+a2b2=0,即 a1b1=-a2b2,.两向量平行的条件是相应坐标成比例,所以(a1,a2)与(-b2,b1)平行,特别地,向量 k(-b2,b1)与向量(b1,b2)垂直,k 为任意实数.例如向量(3,4)与向量(-4,3)、(-8,6)、(12,-9)、…都垂直.疑难疏引设 a=(a1,a2),b=(b1,b2),a1b1+a2b2=0a⊥b 且 a⊥ba1b1+a2b2=0.3.向量的长度、距离和夹角公式(1)已知 a=(a1,a2),则|a|2=a2=a12+a22,即|a|=.语言描述为向量的长度等于它的坐标平方和的算术平方根.若 A(x1,y1),B(x2,y2),则=(x2-x1,y2-y1),||=.此式可视为 A、B 两点的距离公式.(2)设向量 a=(a1,a2),b=(b1,b2),故 cos〈a,b〉=.特别提示:该处夹角公式是非零向量的夹角公式.活学巧用1.设 a=(4,-3),b=(2,1),若 a+tb 与 b 的夹角为 45°,求实数 t 的值.解析:利用 a·b=|a|·|b|·cosθ 建立方程,解方程即可.a+tb=(4,-3)+t(2,1)=(4+2t,t-3),(a+tb)·b=(4+2t,t-3)·(2,1)=5t+5,|a+tb|=,由(a+tb)·b=|a+tb|·|b|·cos45°得 5t+5=,即 t2+2t-3=0,∴t=-3 或 t=1.经检验 t=-3 不合题意,舍去,只取 t=1.2.已知点 A(2,3),若把向量绕原点 O 按逆时针旋转 90°得向量,求点 B 的坐标.解析:要求点 B 的坐标,可设为 B(x,y),利用⊥,| |=||列方程解决之.设点 B 坐标为(x,y),因为⊥,| |=||,所以解得或(舍去).所以 B 点坐标为(-3,2).3.已知 a=(2,-4),b=(1,1),求 a 与 b 的夹角 θ.解析:向量坐标已知,可利用夹角坐标公式解决.a·b=(2,-4)·(1,1)=2+-4=-2,|a|·|b|=∴cosθ=.又 0°≤θ≤180°,∴θ=60°.4.已知 a+b+c=0,|a|=3,|b|=5,|c|=7,求〈a,b〉的值.解析:∵a+b+c=0,∴a+b=-c.∴|a+b|=|c|.∴(a+b)2=c2,即 a2+2a·b+b2=c2.∴a·b=.∴cos〈a,b〉=÷(3×5)= .∴〈a,b〉=.