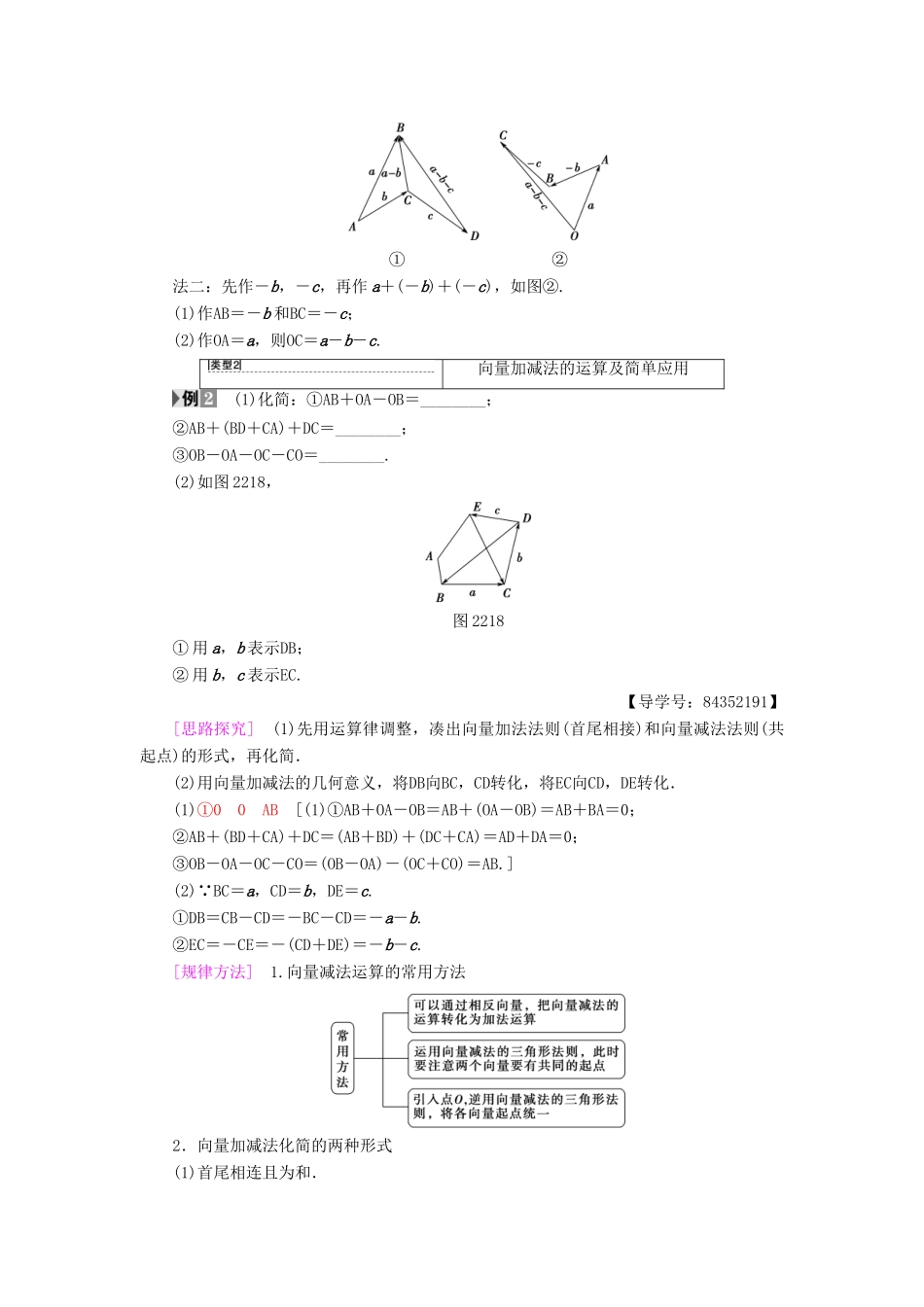
2.2.2 向量减法运算及其几何意义学习目标:1.理解相反向量的含义,能用相反向量说出向量相减的意义.(难点)2.掌握向量减法的运算及其几何意义,能熟练地进行向量的加减运算.(重点)3.能将向量的减法运算转化为向量的加法运算.(易混点)[自 主 预 习·探 新 知]1.相反向量(1)定义:如果两个向量长度相等,而方向相反,那么称这两个向量是相反向量.(2)性质:①对于相反向量有:a+(-a)=0.② 若 a,b 互为相反向量,则 a=-b,a+b=0.③ 零向量的相反向量仍是零向量.2.向量的减法(1)定义:a-b=a+(-b),即减去一个向量相当于加上这个向量的相反向量.(2)作法:在平面内任取一点 O,作OA=a,OB=b,则向量 a-b=BA,如图 2213 所示.图 2213[基础自测]1.思考辨析(1)若 b 是 a 的相反向量,则 a 与 b 一定不相等.( )(2)若 b 是 a 的相反向量,则 a∥b.( )(3)向量AB的相反向量是BA,且BA=-AB.( )(4)PA-PB=AB.( )[解析] (1)错误.当 a=0 时,a 的相反向量也是零向量即 a=b.(2)正确;(3)正确.(4)错误.PA-PB=BA.[答案] (1)× (2)√ (3)√ (4)×2.化简OP-QP+PS+SP的结果等于( )A.QP B.OQC.SP D.SQB [原式=(OP+PQ)+(PS+SP)=OQ+0OQ.]3.如图 2214,在▱ABCD 中,AB=a,AD=b,用 a,b 表示向量AC,BD,则AC=________,BD=________.图 2214a+b,b-a [由向量加法的平行四边形法则,及向量减法的运算法则可知AC=a+b,BD=b-a.][合 作 探 究·攻 重 难]向量减法的几何意义 (1)如图 2215 所示,四边形 ABCD 中,若AB=a,AD=b,BC=c,则DC=( )A.a-b+cB.b-(a+c)C.a+b+cD.b-a+c(2)如图 2216 所示,已知向量 a,b,c 不共线,求作向量 a+b-c. 【导学号:84352190】图 2215 图 2216[思路探究] (1)利用向量减法和加法的几何意义,将DC向AB,BC,AD转化;(2)利用几何意义法与定义法求出 a+b-c 的值.(1)A [DC=AC-AD=(AB+BC)-AD=a+c-b.](2)法一:(几何意义法)如图①所示,在平面内任取一点 O,作OA=a,AB=b,则OB=a+b,再作OC=c,则CB=a+b-c.法二:(定义法)如图②所示,在平面内任取一点 O,作OA=a,AB=b,则OB=a+b,再作BC=-c,连接 OC,则OC=a+b-c.图① 图②[规律方法] 求作两个向量的差向量的两种思路1 可以转化为向量的加法来进行,如 a-b,可以先作-b,然后作 a+-b即可.2...