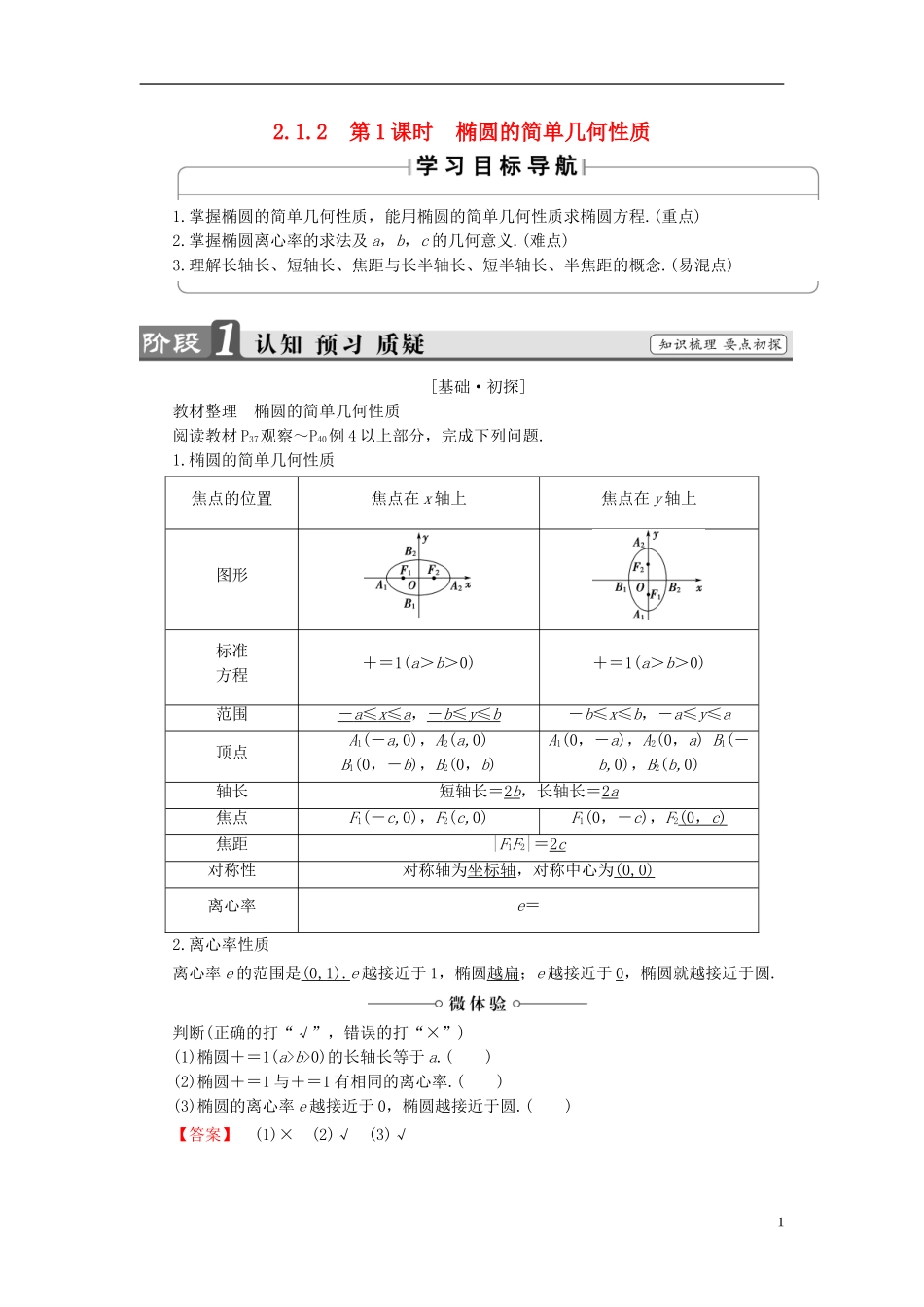
2.1.2 第 1 课时 椭圆的简单几何性质1.掌握椭圆的简单几何性质,能用椭圆的简单几何性质求椭圆方程.(重点)2.掌握椭圆离心率的求法及 a,b,c 的几何意义.(难点)3.理解长轴长、短轴长、焦距与长半轴长、短半轴长、半焦距的概念.(易混点)[基础·初探]教材整理 椭圆的简单几何性质阅读教材 P37观察~P40例 4 以上部分,完成下列问题.1.椭圆的简单几何性质焦点的位置焦点在 x 轴上焦点在 y 轴上图形标准方程+=1(a>b>0)+=1(a>b>0)范围- a ≤ x ≤ a ,- b ≤ y ≤ b -b≤x≤b,-a≤y≤a顶点A1(-a,0),A2(a,0) B1(0,-b),B2(0,b)A1(0,-a),A2(0,a) B1(-b,0),B2(b,0)轴长短轴长=2 b ,长轴长=2 a 焦点F1(-c,0),F2(c,0)F1(0,-c),F2(0 , c ) 焦距|F1F2|=2 c 对称性对称轴为坐标轴,对称中心为(0,0)离心率e=2.离心率性质离心率 e 的范围是(0,1).e 越接近于 1,椭圆越扁;e 越接近于 0,椭圆就越接近于圆.判断(正确的打“√”,错误的打“×”)(1)椭圆+=1(a>b>0)的长轴长等于 a.( )(2)椭圆+=1 与+=1 有相同的离心率.( )(3)椭圆的离心率 e 越接近于 0,椭圆越接近于圆.( )【答案】 (1)× (2)√ (3)√1[小组合作型]椭圆的简单几何性质 (1)椭圆以两条坐标轴为对称轴,一个顶点是(0,13),另一个顶点是(-10,0),则焦点坐标为( )A.(±13,0)B.(0,±10)C.(0,±13)D.(0,±)(2)如果一个椭圆的长轴长是短轴长的两倍,那么这个椭圆的离心率为( )A.B.C.D.【自主解答】 (1)由题意知椭圆焦点在 y 轴上,且 a=13,b=10,则 c==,故焦点坐标为(0,±).(2)设长轴长为 2a,短轴长为 2b,由题意可知 a=2b,则 c===b,所以离心率为 e===.【答案】 (1)D (2)B已知椭圆的方程讨论其几何性质时,应先将方程化为标准形式,不确定焦点位置的要分类讨论,找准 a 和 b,才能正确地写出焦点坐标、顶点坐标等,同时,要注意其中某些概念的区别,如长轴长是 2a,短轴长是 2b.[再练一题]1.(1)椭圆 6x2+y2=6 的长轴的顶点坐标是( )A.(-1,0),(1,0)B.(-6,0),(6,0)C.(-,0),(,0)D.(0,-),(0, )【解析】 椭圆的标准方程为 x2+=1,焦点在 y 轴上,其长轴的端点坐标为(0,±).【答案】 D(2)已知椭圆+=1 的一个顶点为(0,5),试求椭圆的长轴长,短轴长,焦点坐标,离心率及其余的顶点.【解】 (0,5)是椭圆+=1 的顶点,∴m=25.∴椭圆方...