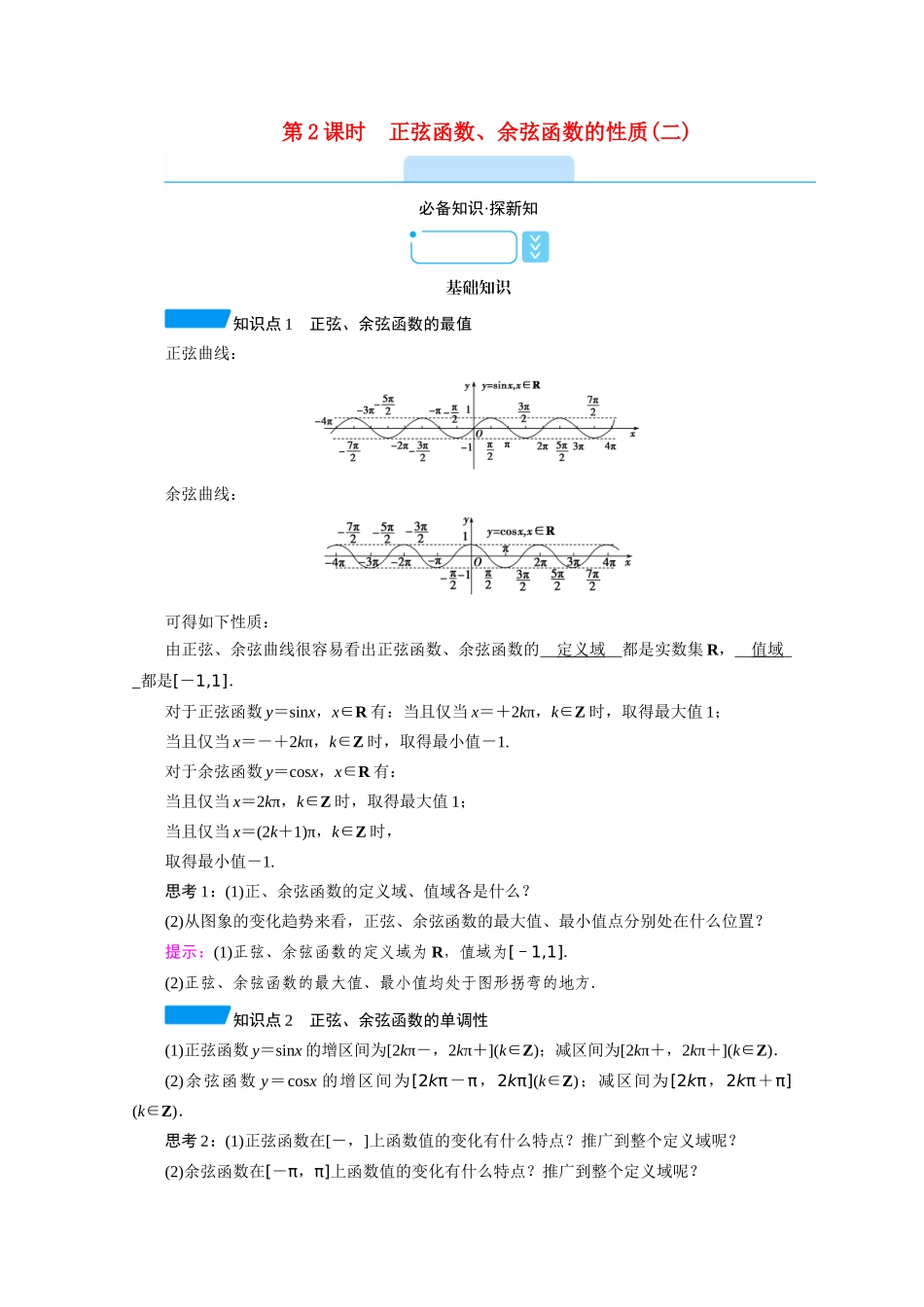
第 2 课时 正弦函数、余弦函数的性质(二)必备知识·探新知基础知识知识点 1 正弦、余弦函数的最值正弦曲线:余弦曲线:可得如下性质:由正弦、余弦曲线很容易看出正弦函数、余弦函数的__定义域__都是实数集 R,__值域__都是[-1,1].对于正弦函数 y=sinx,x∈R 有:当且仅当 x=+2kπ,k∈Z 时,取得最大值 1;当且仅当 x=-+2kπ,k∈Z 时,取得最小值-1.对于余弦函数 y=cosx,x∈R 有:当且仅当 x=2kπ,k∈Z 时,取得最大值 1;当且仅当 x=(2k+1)π,k∈Z 时,取得最小值-1.思考 1:(1)正、余弦函数的定义域、值域各是什么?(2)从图象的变化趋势来看,正弦、余弦函数的最大值、最小值点分别处在什么位置?提示:(1)正弦、余弦函数的定义域为 R,值域为[-1,1].(2)正弦、余弦函数的最大值、最小值均处于图形拐弯的地方.知识点 2 正弦、余弦函数的单调性(1)正弦函数 y=sinx 的增区间为[2kπ-,2kπ+](k∈Z);减区间为[2kπ+,2kπ+](k∈Z).(2)余弦函数 y=cosx 的增区间为[2kπ-π,2kπ](k∈Z);减区间为[2kπ,2kπ+π](k∈Z).思考 2:(1)正弦函数在[-,]上函数值的变化有什么特点?推广到整个定义域呢?(2)余弦函数在[-π,π]上函数值的变化有什么特点?推广到整个定义域呢?提示:(1)观察图象可知:当 x∈[-,]时,曲线逐渐上升,是增函数,sinx 的值由-1 增大到 1;当 x∈[,]时,曲线逐渐下降,是减函数,sinx 的值由 1 减小到-1.推广到整个定义域可得当 x∈[-+2kπ,+2kπ](k∈Z)时,正弦函数 y=sinx 是增函数,函数值由-1 增大到 1;当 x∈[+2kπ,+2kπ](k∈Z)时,正弦函数 y=sinx 是减函数,函数值由 1 减小到-1.(2)观察图象可知:当 x∈[-π,0]时,曲线逐渐上升,是增函数,cosx 的值由-1 增大到 1;当 x∈[0,π]时,曲线逐渐下降,是减函数,cosx 的值由 1 减小到-1.推广到整个定义域可得当 x∈[2kπ-π,2kπ],k∈Z 时,余弦函数 y=cosx 是增函数,函数值由-1 增大到 1;当 x∈[2kπ,(2k+1)π],k∈Z 时,余弦函数 y=cosx 是减函数,函数值由 1 减小到-1.基础自测1.在下列区间中,使函数 y=sinx 为增函数的是( C )A.[0,π]B.[,]C.[-,]D.[π,2π]2.下列函数中在上是增函数的是( D )A.y=sinxB.y=cosxC.y=sin2xD.y=cos2x[解析] y=sinx 在上是减函数,不满足条件.y=cosx 在上是...