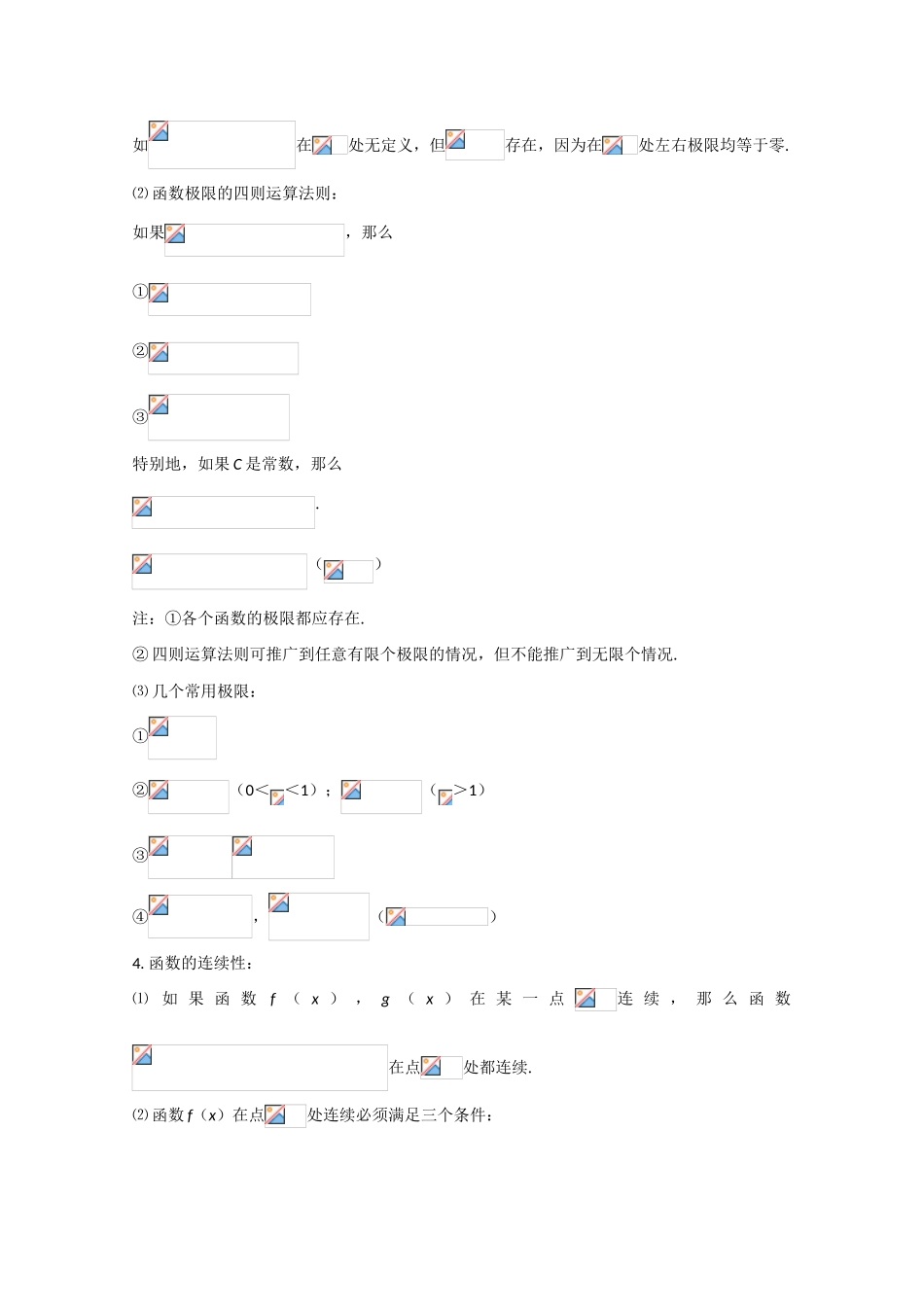
高中数学第十三章-极 限极 限考试内容: 教学归纳法.数学归纳法应用. 数列的极限. 函数的极限.根限的四则运算.函数的连续性.考试要求:(1)理解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题.(2)了解数列极限和函数极限的概念.(3)掌握极限的四则运算法则;会求某些数列与函数的极限.(4)了解函数连续的意义,了解闭区间上连续函数有最大值和最小值的性质.§13. 极 限极 限 知识要点知识要点1. ⑴ 第一数学归纳法:①证明当取第一个时结论正确;②假设当()时,结论正确,证明当时,结论成立.⑵ 第二数学归纳法:设是一个与正整数有关的命题,如果① 当()时,成立;② 假设当()时,成立,推得时,也成立.那么,根据①②对一切自然数时,都成立.2. ⑴ 数列极限的表示方法:①② 当时,.⑵ 几个常用极限:①(为常数)②③ 对于任意实常数,当时,当时,若 a = 1,则;若,则不存在当时,不存在⑶ 数列极限的四则运算法则:如果,那么①②③特别地,如果 C 是常数,那么.⑷ 数列极限的应用:求无穷数列的各项和,特别地,当时,无穷等比数列的各项和为.(化循环小数为分数方法同上式)注:并不是每一个无穷数列都有极限.3. 函数极限;⑴ 当自变量无限趋近于常数(但不等于)时,如果函数无限趋进于一个常数,就是说当趋近于时,函数的极限为.记作或当时,.注:当时,是否存在极限与在处是否定义无关,因为并不要求.(当然,在是否有定义也与在处是否存在极限无关.函数在有定义是存在的既不充分又不必要条件.)如在处无定义,但存在,因为在处左右极限均等于零.⑵ 函数极限的四则运算法则:如果,那么①②③特别地,如果 C 是常数,那么.()注:①各个函数的极限都应存在.② 四则运算法则可推广到任意有限个极限的情况,但不能推广到无限个情况.⑶ 几个常用极限:①②(0<<1);(>1)③④,()4. 函数的连续性:⑴如 果 函 数f ( x ) , g ( x ) 在 某 一 点连 续 , 那 么 函 数在点处都连续.⑵ 函数 f(x)在点处连续必须满足三个条件:① 函数 f(x)在点处有定义;②存在;③函数 f(x)在点处的极限值等于该点的函数值,即.⑶ 函数 f(x)在点处不连续(间断)的判定:如果函数 f(x)在点处有下列三种情况之一时,则称为函数 f(x)的不连续点.①f(x)在点处没有定义,即不存在;②不存在;③存在,但.5. 零点定理,介值定理,夹...